题目内容

2、函数f（x）的导函数为f′（x）=x（1-x），则f（x）的单调递增区间为（　　）
分析：已知导函数为f′（x）=x（1-x），令f′（x）≥0，解出x的范围，和定义域求交集即可
解答：解：令f′（x）≥0，得x（1-x）≥0，
解得0≤x≤1，又定义域为R，
f（x）的单调递增区间为[0，1]；
故选C
点评：本题考查利用导数求函数单调区间，注意定义域，这是学生忽视的地方
练习册系列答案
相关题目
精英家教网已知函数f（x）的定义域为[-2，+∞），部分对应值如下表，
 x -2    0 4
f（x）   1 -1 1
f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示：若两正数a，b满足f（2a+b）＜1，则
b+3
a+3
的取值范围是（　　）
A、(
6
7
，
4
3
)
B、(
3
5
，
7
3
)
C、(
2
3
，
6
5
)
D、（-
1
3
，3）
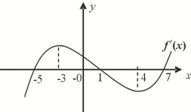4、已知函数f（x）的导函数的图象如图所示，给出下列四个结论：
①函数f（x）在区间（-3，1）内单调递减；
②函数f（x）在区间（1，7）内单调递减；
③当x=-3时，函数f（x）有极大值；
④当x=7时，函数f（x）有极小值．
则其中正确的是（　　）
（2013•中山一模）已知函数f(x)=
13
x3-ax+b，其中实数a，b是常数．
（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．
（2010•合肥模拟）已知向量
a
=(sinx，cosx)，
b
=(cosx，
3
cosx)，f(x)=
a
•
b
-
3
2
，下面关于函数f（x）的导函数f'（x）说法中错误的是（　　）
已知函数f(x)=
1
3
x3-ax+b，其中实数a，b是常数．
（Ⅰ）已知a∈{0，1，2}，b∈{0，1，2}，求事件A：“f（1）≥0”发生的概率；
（Ⅱ）若f（x）是R上的奇函数，g（a）是f（x）在区间[-1，1]上的最小值，求当|a|≥1时g（a）的解析式；
（Ⅲ）记y=f（x）的导函数为f′（x），则当a=1时，对任意x1∈[0，2]，总存在x2∈[0，2]使得f（x1）=f′（x2），求实数b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网