题目内容
已知斜率为k(k≠0)的直线l过抛物线C:y2=4x的焦点F且交抛物线于A、B两点.设线段AB的中点为M.
(1)求点M的轨迹方程;
(2)若﹣2<k<﹣1时,点M到直线l':3x+4y﹣m=0(m为常数,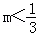 )的距离总不小于
)的距离总不小于 ,求m的取值范围.
,求m的取值范围.
(1)求点M的轨迹方程;
(2)若﹣2<k<﹣1时,点M到直线l':3x+4y﹣m=0(m为常数,
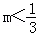 )的距离总不小于
)的距离总不小于 ,求m的取值范围.
,求m的取值范围.解:(1)设AB的中点为O(x,y);A(x1,y1),B(x2,y2),
∵直线过抛物线y2=4x得焦点F(1,0),
∴设直线的方程为:y=k(x﹣1),①
将①2代入抛物线方程中可得:k2(x﹣1)2=4x,
∴k2x2﹣(2k2+4)x+k2=0,②
∴x1+x2= (2k2+4)=2+
(2k2+4)=2+ ,
,
∵y1+y2=k(x1+x2﹣2)= ,
,
又∵x= =1+
=1+ ,…③
,…③
y= =
= ,
,
∴ ,…④
,…④
∴将④代入③可得:x=1+ ,
,
∴y2=2x﹣2.
所以点M的轨迹方程为:y2=2x﹣2.
(2)由(1)知,点M( ,
, ),
),
∵M( ,
, )到直线l':3x+4y﹣m=0的距离d=
)到直线l':3x+4y﹣m=0的距离d= ,
,
∴点M到直线l':3x+4y﹣m=0(m为常数, )的距离总不小于
)的距离总不小于 ,
,
∴
 ,
,
∴ ,或
,或 ,
,
即 ,或
,或 ,
,
∴﹣2<k<﹣1,∴﹣ <
< <4,
<4,
 ,
,
∴m ,或m≥6,
,或m≥6,
∴m< ,
,
∴m≤﹣ .
.
故m的取值范围是{m|m≤﹣ }.
}.
∵直线过抛物线y2=4x得焦点F(1,0),
∴设直线的方程为:y=k(x﹣1),①
将①2代入抛物线方程中可得:k2(x﹣1)2=4x,
∴k2x2﹣(2k2+4)x+k2=0,②
∴x1+x2=
 (2k2+4)=2+
(2k2+4)=2+ ,
,∵y1+y2=k(x1+x2﹣2)=
 ,
,又∵x=
 =1+
=1+ ,…③
,…③y=
 =
= ,
,∴
 ,…④
,…④∴将④代入③可得:x=1+
 ,
,∴y2=2x﹣2.
所以点M的轨迹方程为:y2=2x﹣2.
(2)由(1)知,点M(
 ,
, ),
),∵M(
 ,
, )到直线l':3x+4y﹣m=0的距离d=
)到直线l':3x+4y﹣m=0的距离d= ,
,∴点M到直线l':3x+4y﹣m=0(m为常数,
 )的距离总不小于
)的距离总不小于 ,
,∴

 ,
,∴
 ,或
,或 ,
,即
 ,或
,或 ,
,∴﹣2<k<﹣1,∴﹣
 <
< <4,
<4, ,
,∴m
 ,或m≥6,
,或m≥6,∴m<
 ,
,∴m≤﹣
 .
.故m的取值范围是{m|m≤﹣
 }.
}.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
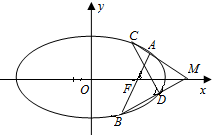 已知椭圆G:
已知椭圆G: