题目内容
已知函数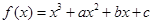 在
在 与
与 时都取得极值.
时都取得极值.
(1)求 的值与函数
的值与函数 的单调区间
的单调区间
(2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1) ,函数
,函数 的递增区间是
的递增区间是 与
与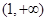 ,递减区间是
,递减区间是 ;(2)
;(2) 或
或 .
.
解析试题分析:(1)先求出 ,进而得到
,进而得到 ,从中解方程组即可得到
,从中解方程组即可得到 的值,然后再通过
的值,然后再通过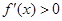 求出函数
求出函数 的增区间,通过
的增区间,通过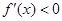 求出函数
求出函数 的减区间; (2)要使对
的减区间; (2)要使对 ,不等式
,不等式 恒成立问题,则只需
恒成立问题,则只需 ,从而目标转向函数
,从而目标转向函数 的最大值,根据(1)中所得的
的最大值,根据(1)中所得的 值,确定函数
值,确定函数 在区间
在区间 的最大值,进而求解不等式
的最大值,进而求解不等式 即可.
即可.
试题解析:(1)
由 ,
, 得
得
 ,函数
,函数 的单调区间如下表:
的单调区间如下表:
所以函数 



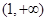







极大值 ¯ 极小值  的递增区间是
的递增区间是

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
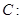
 的左焦点为
的左焦点为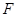 ,左、右顶点分别为
,左、右顶点分别为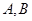 ,过点
,过点 的直线
的直线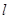 交椭圆于
交椭圆于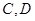 两点,椭圆
两点,椭圆 的离心率为
的离心率为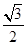 ,
,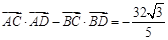 .
.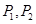 是椭圆上不同两点,
是椭圆上不同两点,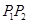
 轴,圆
轴,圆 过点
过点 ,在
,在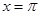 处取最小值.
处取最小值. 的值;
的值; 中,
中, 分别是
分别是 的对边,已知
的对边,已知 ,求角
,求角 .
. 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当
 的单调性;
的单调性;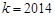 时,关于
时,关于 的方程
的方程 有唯一解,求
有唯一解,求 的值;
的值; 时,证明: 对一切
时,证明: 对一切 ,都有
,都有 成立.
成立. ,
, .
. 的最小正周期和值域;
的最小正周期和值域; ,且
,且 ,求
,求 的值.
的值. 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域 内,乙中转站建在区域
内,乙中转站建在区域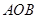 内.分界线
内.分界线 固定,且
固定,且 百米,边界线
百米,边界线 始终过点
始终过点 ,边界线
,边界线 满足
满足 .
. (
( )百米,
)百米,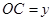 百米.
百米.
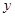 表示成
表示成 的函数,并求出函数
的函数,并求出函数 最小,并求出其面积的最小值.
最小,并求出其面积的最小值. -4
-4 +2的最大值和最小值.
+2的最大值和最小值.