题目内容
已知Rt△ABC的斜边BC=5，则| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
分析：看清各个量之间的关系，代入数量积的公式，整理所得的算式，要注意向量的夹角是内角的补角，正弦定理的应用也是一个难点，根据同角的三角函数关系的变化也要注意．
解答：解：设AC=b，AB=c，
原式=5bcos（180°-C）+0+5ccos（180°-B）
=-5bcosC-5ccosB
=-5（asinA+csinC）
=-5（2Rsin2A+2Rsin2B）
=-5×2R，
∵R是三角形外接圆的半径，
∴2R=5，
∴原式=-25，
故答案为：-25．
原式=5bcos（180°-C）+0+5ccos（180°-B）
=-5bcosC-5ccosB
=-5（asinA+csinC）
=-5（2Rsin2A+2Rsin2B）
=-5×2R，
∵R是三角形外接圆的半径，
∴2R=5，
∴原式=-25，
故答案为：-25．
点评：本题是向量数量积的运算，条件中给出两个向量的模和两向量的夹角，代入数量积的公式运算即可，只是题目所给的模不是数字，而是用三角函数表示的式子，因此代入后，还要进行简单的三角函数变换和应用正弦定理．
练习册系列答案
相关题目
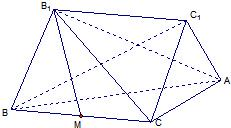如图：已知BB1，CC1是Rt△ABC所在平面同侧的两条相等的斜线段，它们与平面ABC所成的角均为60°，且BB1∥CC1，线段BB1的端点B1在平面ABC的射影M恰是BC的中点，已知BC=2，∠ACB=90°
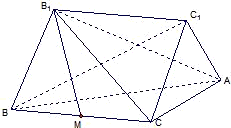如图：已知BB1，CC1是Rt△ABC所在平面同侧的两条相等的斜线段，它们与平面ABC所成的角均为60°，且BB1∥CC1，线段BB1的端点B1在平面ABC的射影M恰是BC的中点，已知BC=2，∠ACB=90°