题目内容
对于非空实数集合 ,记
,记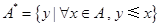 ,设非空实数集合
,设非空实数集合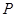 满足条件“若
满足条件“若 ,则
,则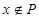 ”且
”且 ,给出下列命题:
,给出下列命题:
①若全集为实数集 ,对于任意非空实数集合
,对于任意非空实数集合 ,必有
,必有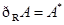 ;
;
②对于任意给定符合题设条件的集合
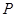 ,必有
,必有 ;
;
③存在符合题设条件的集合
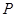 ,使得
,使得 ;
;
④存在符合题设条件的集合
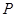 ,使得
,使得 .
.
其中所有正确命题的序号是 .
②③④
解析试题分析:由题意 *中元素为不大于
*中元素为不大于 中所有值的数,即不大于
中所有值的数,即不大于 中最小元素的集合.①当
中最小元素的集合.①当 集合下边界趋向负无穷大时,假设
集合下边界趋向负无穷大时,假设 ,则
,则 ,
, ,易知
,易知 故①错误;②由于
故①错误;②由于 ,假设
,假设 中最小值为
中最小值为 ,
, 中最小值为
中最小值为 ,那么
,那么 ≥
≥ .因此
.因此 表示小于等于
表示小于等于 所有数集合,
所有数集合, 表示所有小于等于
表示所有小于等于 的数的集合.则
的数的集合.则 ,故②正确;③令
,故②正确;③令 ,则
,则 ,所以
,所以 ,故③正确;④令
,故③正确;④令 ,
, ,则
,则 ,所以
,所以 ,故④正确.故答案为:②③④.
,故④正确.故答案为:②③④.
考点:元素与集合关系的判断.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 ,集合
,集合 ,则
,则 .
. ,且
,且 ,则实数
,则实数 的取值范围是 .
的取值范围是 . ,
, ,则
,则 =_____
=_____ ,则
,则 = .
= . },B={
},B={ },则
},则 =
=  ,
, ,若
,若 ,则实数a的取值范围是 .
,则实数a的取值范围是 . <x<
<x<