Question

已知函数f（x）的定义域为[-2，+∞），且f（4）=f（-2）=1，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示．则平面区域

a≥0 b≥0 f(2a+b)＜1

所围成的面积是（　　）

A．2

B．3

C．4

D．5

Answer 1

分析：由函数y=f′（x）的图象可得：当x∈（0，+∞）时，f′（x）＞0，此时函数f（x）单调递增．由f（2a+b）＜1，f（4）=1，及f（2a+b）＜1=f（4）．
可得2a+b＜4．再利用线性规划的有关知识即可得出．

解答：解：由函数y=f′（x）的图象可得：当x∈[-2，0）]时，f′（x）＜0，此时函数f（x）单调递减；当x∈（0，+∞）时，f′（x）＞0，此时函数f（x）单调递增．
∵a≥0，b≥0，∴2a+b≥0．
又∵f（4）=1，f（2a+b）＜1，
∴f（2a+b）＜f（4）．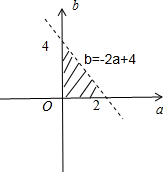
∴0≤2a+b＜4．
由

a≥0 b≥0 0≤2a+b＜4

，画出图象如图
∴阴影部分的面积S=

1

2

×2×4=4．
故选C．

点评：本题考查了利用导数研究函数的单调性、数形结合的思想方法、线性规划的有关知识等基础知识与基本方法，属于中档题．