题目内容
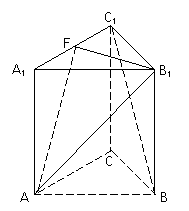
如图,在正三棱柱(底面为正三角形,侧棱与底面垂直的棱柱)ABC―A1B1C1中,F是A1C1的中点,
(1)求证:BC1//平面AFB1 w.w.w.k.s.5.u.c.o.m ![]()
![]()
 (2)求证:平面AFB1⊥平面ACC1A1
(2)求证:平面AFB1⊥平面ACC1A1
(3)作出平面AFB1与平面BCC1B1 的交线![]()
 解析:(1)连A1B交A B1于点G,连接GF
解析:(1)连A1B交A B1于点G,连接GF
∵正三棱柱ABC―A1B1C1的侧面A1B1 BA是矩形
∴对角线互相平分,即点G为A1B的中点
又△A1BC1中,点F是A1C1的中点
∴GF是△A1BC1的中位线,即GF∥B C1 ……2分
又B C1![]() 平面AF B1,GF
平面AF B1,GF![]() 平面AF B1 ……4分
平面AF B1 ……4分
∴B C1∥平面A F B1 ……5分
(2)∵三棱柱ABC―A1B1C1为正三棱柱
∴A A1⊥平面A1B1C1
又B1F![]() 平面A1B1C1, ∴B1F⊥A A1
平面A1B1C1, ∴B1F⊥A A1
又点F为正△A1B1C1边A1C1上的中点
∴B1F⊥A1C1 ……7分
又直线A1C1、A A1是平面AC C1A1中的两相交直线
∴B1F⊥平面AC C1A1 ……9分
又B1F![]() 平面A F B1
平面A F B1
∴平面A F B1⊥平面AC C1A1 ……10分
(3)延长AF交CC1的延长线于点H,连接B1H,则直线B1H就是平面AFB1与平面BCC1B1 的交线![]() 。……12分
。……12分
证明如下:
∵点B1和H为平面AFB1与平面BCC1B1 的公共点
∴B1H![]() 平面AFB1,B1H
平面AFB1,B1H![]() 平面BCC1B1
平面BCC1B1
∴平面AFB1![]() 平面BCC1B1 = B1H
平面BCC1B1 = B1H
即B1H就是平面AFB1与平面BCC1B1 的交线![]() ……14分
……14分 w
w

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点
已知(如图)在正三棱柱(底面正三角形,侧棱垂直于底面)ABC-A1B1C1中,若AB=AA1=4,点D是AA1的中点,点P是BC1中点 如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,F是A1C1的中点.
如图,在正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1中,F是A1C1的中点.
