题目内容
设数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() ,
,![]() .(1)求
.(1)求![]() ,
,![]() 的值;(2)求数列
的值;(2)求数列![]() 的通项公式
的通项公式![]() ;(3)证明:
;(3)证明:![]() .
.
(本小题主要考查数列、不等式、二项式定理等知识,考查化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识)
(1)解:当![]() 时,有
时,有![]() ,
,
由于![]() ,所以
,所以![]() .
.
当![]() 时,有
时,有![]() ,即
,即![]() ,
,
将![]() 代入上式,由于
代入上式,由于![]() ,所以
,所以![]() .
.
(2)解:由![]() ,
,
得![]() ,
, ![]() ①
①
则有![]() . ②
. ②
②-①,得![]() ,
,
由于![]() ,所以
,所以![]() . ③
. ③
同样有![]()
![]() , ④
, ④
③-④,得![]() .
.
所以![]() .
.
由于![]() ,即当
,即当![]() 时都有
时都有![]() ,所以数列
,所以数列![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
故![]() .
.
(3)证明1:由于![]() ,
,
![]() ,
,
所以![]() .
.
即![]() .
.
令![]() ,则有
,则有![]() .
.
即![]() ,
,
即![]()
故![]() .
.![]()
证明2:要证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
只需证![]()
![]() .
.
由于![]()
![]()
![]()
![]() .
.
因此原不等式成立.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. ,数列
,数列 的前
的前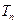 ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. 与
与 两项之间插入
两项之间插入 个数构成等差数列,其公差为
个数构成等差数列,其公差为 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且满足
,且满足
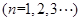 .
. 为等比数列;
为等比数列; ;
; 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列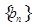 的前
的前 .
. 
 的前
的前 项和为
项和为 ,且
,且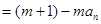 对于
对于 为常数,且
为常数,且
 ,数列
,数列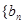

 ,
,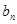
 )(
)( ,
, ,求证:数列
,求证:数列

