题目内容
已知函数f(x)=|x2-2|,若f(a)≥f(b),且0≤a≤b,则满足条件的点(a,b)所围成区域的面积为______.
∵由f(x)=|x2-2|,结合f(a)≥f(b)得出(a2-2)2-(b2-2)2≥0,分解为(a2+b2-4)(a-b)(a+b)≥0,
可得约束条件:
|
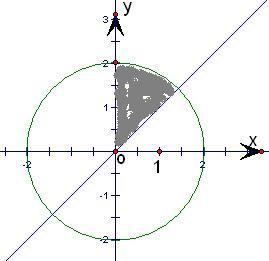
其对应的可行域为扇形,如下图示:
其大小为八分之一个圆.
故所求面积为:S=
| 1 |
| 8 |
| π |
| 2 |
故答案为:
| π |
| 2 |

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|