题目内容
如图4,在一面南北方向的长方形墙ABHG上用AC=3m,BC=4m,AB=5m的角钢焊接成一个简易的遮阳棚(将AB放在墙上)。一般认为,从正西方向射出的太阳光线与地面成75°角时气温最高。要使此时遮阳棚的遮阴面积最大,应将遮阳棚ABC面与水平面成多大角度?

墙面ABHG在太阳光照射下的射影为 ,由题意可知光线
,由题意可知光线 与地面所成的角为750,设遮阳棚ABC面与地面所成的角为θ(00≤θ≤900),△ABC在地面上的射影为△
与地面所成的角为750,设遮阳棚ABC面与地面所成的角为θ(00≤θ≤900),△ABC在地面上的射影为△ ,要使此时遮阳棚的遮阴面积最大,即△
,要使此时遮阳棚的遮阴面积最大,即△ 的面积最大,在
的面积最大,在 上取一点D,使
上取一点D,使 //AC,则易证明面ABC//面
//AC,则易证明面ABC//面 ,且△ABC≌△
,且△ABC≌△ ,在平面
,在平面 内作DM⊥
内作DM⊥ ,垂足为M,连C/M,∵AB⊥CC/,∴
,垂足为M,连C/M,∵AB⊥CC/,∴ ⊥
⊥ ,∴C/M⊥
,∴C/M⊥ ,则平面
,则平面 与地面所成的二面角的大小为∠DMC/=θ,又由已知条件可得△
与地面所成的二面角的大小为∠DMC/=θ,又由已知条件可得△ 为直角三角形,DM=
为直角三角形,DM= m,在△DMC/中,由正弦定理得MC/=
m,在△DMC/中,由正弦定理得MC/= ,∴当
,∴当 =1,即θ=150时,MC/最大,∵
=1,即θ=150时,MC/最大,∵ 为定值,所以此时△
为定值,所以此时△ 的面积最大。
的面积最大。
 ,由题意可知光线
,由题意可知光线 与地面所成的角为750,设遮阳棚ABC面与地面所成的角为θ(00≤θ≤900),△ABC在地面上的射影为△
与地面所成的角为750,设遮阳棚ABC面与地面所成的角为θ(00≤θ≤900),△ABC在地面上的射影为△ ,要使此时遮阳棚的遮阴面积最大,即△
,要使此时遮阳棚的遮阴面积最大,即△ 的面积最大,在
的面积最大,在 上取一点D,使
上取一点D,使 //AC,则易证明面ABC//面
//AC,则易证明面ABC//面 ,且△ABC≌△
,且△ABC≌△ ,在平面
,在平面 内作DM⊥
内作DM⊥ ,垂足为M,连C/M,∵AB⊥CC/,∴
,垂足为M,连C/M,∵AB⊥CC/,∴ ⊥
⊥ ,∴C/M⊥
,∴C/M⊥ ,则平面
,则平面 与地面所成的二面角的大小为∠DMC/=θ,又由已知条件可得△
与地面所成的二面角的大小为∠DMC/=θ,又由已知条件可得△ 为直角三角形,DM=
为直角三角形,DM= m,在△DMC/中,由正弦定理得MC/=
m,在△DMC/中,由正弦定理得MC/= ,∴当
,∴当 =1,即θ=150时,MC/最大,∵
=1,即θ=150时,MC/最大,∵ 为定值,所以此时△
为定值,所以此时△ 的面积最大。
的面积最大。见答案

练习册系列答案
相关题目
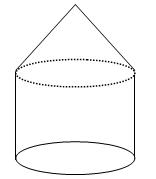
 ),则此几何体的体积是( )
),则此几何体的体积是( )





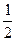 B.
B.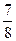 C.
C.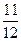 D.
D.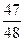

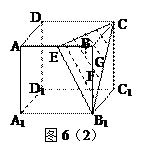
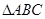 的三边分别为
的三边分别为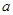 ,
,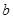 ,
,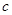 ,
,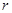 ,则
,则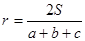 ,类比这个结论可知:四面体
,类比这个结论可知:四面体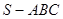 的四个面面积分别为
的四个面面积分别为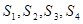 ,内切球半径为
,内切球半径为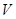 ,则
,则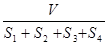




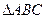 的三个顶点距离均为1cm的平面共有 .
的三个顶点距离均为1cm的平面共有 . 


