题目内容
在数列{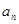 }中,
}中,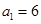 ,且
,且
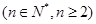 ,
,
(1)求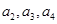 的值;
的值;
(2)猜测数列{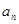 }的通项公式,并用数学归纳法证明。
}的通项公式,并用数学归纳法证明。
(1)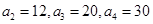 ;(2)详见解析
;(2)详见解析
解析试题分析:(1)根据数列的递推公式将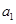 代入可求
代入可求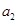 ,同理依次可求出
,同理依次可求出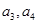 。(2)
。(2)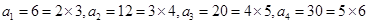 ,
,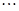 ,猜想
,猜想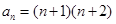 。由(1)知当
。由(1)知当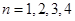 时,显然成立。假设当
时,显然成立。假设当
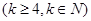 时成立,即有
时成立,即有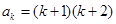 。由已知
。由已知 可知
可知 。则根据
。则根据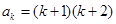 求
求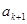 ,并将其整理为
,并将其整理为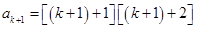 的形式,则说明
的形式,则说明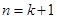 时猜想也成立。从而可证得
时猜想也成立。从而可证得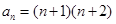 对一切
对一切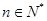 均成立。
均成立。
解:(1)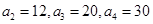 6分
6分
(2)猜测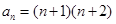 。下用数学归纳法证明:
。下用数学归纳法证明:
①当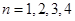 时,显然成立;
时,显然成立;
②假设当
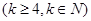 时成立,即有
时成立,即有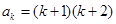 ,则当
,则当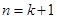 时,由
时,由 得
得 ,
,
故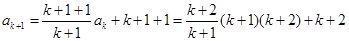
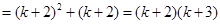 ,故
,故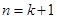 时等式成立;
时等式成立;
③由①②可知,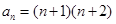 对一切
对一切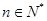 均成立。 13分
均成立。 13分
考点:1递推公式;2数学归纳法。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知等差数列 中,
中, ,那么
,那么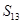 =( )
=( )
| A.390 | B.195 | C.180 | D.120 |
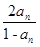 ,则a5= .
,则a5= .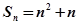 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________ 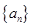 是公比大于1的等比数列,
是公比大于1的等比数列,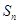 为数列
为数列 项和,已知
项和,已知 ,且
,且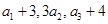 构成等差数列.
构成等差数列.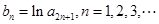 ,求数列
,求数列 的前
的前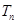 .
.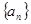 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足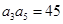 ,
, 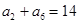 .
. 的通项公式;
的通项公式; 满足:
满足: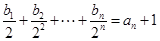
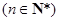 ,求数列
,求数列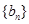 的前
的前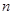 项和.
项和.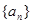 的前
的前 项和
项和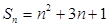 ,则通项
,则通项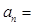
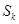 (k=1,2,3,…,n),定义
(k=1,2,3,…,n),定义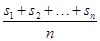 为该项数列的“凯森和”,如果项系数为99项的数列a1,a2,a3,…,a99的“凯森和”为1 000,那么项数为100的数列100,a1,a2,a3,…,a99的“凯森和”为( )
为该项数列的“凯森和”,如果项系数为99项的数列a1,a2,a3,…,a99的“凯森和”为1 000,那么项数为100的数列100,a1,a2,a3,…,a99的“凯森和”为( )