Question

(2004重庆，8)设P是60°的二面角α－l－β内一点，PA⊥平面α，PB⊥平面β，A、B分别为垂足，PA=4，PB=2，则AB的长是

[　　]

A．	B．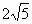
C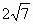．	D．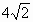

Answer 1

答案：C
解析：

解析：如下图，可设直线l与平面PAB相交于C，由PA⊥面α，PA⊥l，PB⊥面β，PB⊥l，则∠ACB是二面角α－l－β的平面角为60°，由P、A、B、C四点共圆可得∠APB=120°，故由余弦定理知AB=，故选C．

提示：

剖析：可以证明l垂直平面PAB，从而平面PAB和二面角的两个面的交线所成的角就是二面角α－l－β的平面角．从而可解决本问题．