题目内容
设P:二次函数 在区间
在区间 上存在零点;Q:函数
上存在零点;Q:函数 在
在 内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数
内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数 的取值范围.
的取值范围.
 在区间
在区间 上存在零点;Q:函数
上存在零点;Q:函数 在
在 内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数
内没有极值点.若“P或Q”为真命题,“P且Q”为假命题,求实数 的取值范围.
的取值范围.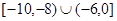 。
。试题分析:先求出p,q为真时对应的a的取值范围,然后根据“P或Q”为真命题,“P且Q”为假命题确定p,q一真一假,从而分两种情况:p真q假或p假q真两种情况研究出a的取值范围,最后求并集即可.
因为函数
 的对称轴是x=2,所以f(x)在区间[-1,1]上是减函数.又函数在区间[-1,1]上存在零点,则必有
的对称轴是x=2,所以f(x)在区间[-1,1]上是减函数.又函数在区间[-1,1]上存在零点,则必有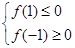 ,…………………2分
,…………………2分即
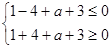 ,解得:
,解得: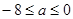 .
.即P:
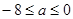 .
.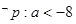 ,或
,或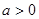 ………………………4分
………………………4分又函数
 在
在 内没有极值点,则函数
内没有极值点,则函数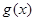 在
在 上是单调函数,而
上是单调函数,而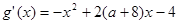 ,需
,需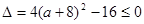 ,解得:
,解得: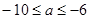
即Q:
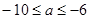 .
. Q:
Q: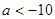 或
或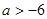 …………8分
…………8分由题设“P或Q”为真命题,“P且Q”为假命题知:p、Q一真一假…………9分
①当p真Q假时,需
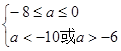 得:
得: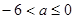 ………………10分
………………10分②当p 假Q真时,需
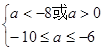 得:
得: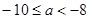 ………………12分
………………12分综上,实数
 的取值范围为
的取值范围为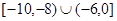 ……………………13分
……………………13分点评:复合命题真假判定方法:或命题是有真则真;且命题是有假则假,非命题是真假相反.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 的零点的个数是 .
的零点的个数是 . cos2x在区间[-3,3]上的零点的个数为( )
cos2x在区间[-3,3]上的零点的个数为( )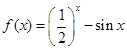 ,则
,则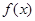 在
在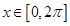 上的零点个数为 ( )
上的零点个数为 ( )  唯一的零点在区间
唯一的零点在区间 、
、 、
、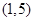 内,那么下面命题错误的
内,那么下面命题错误的 或
或 内有零点
内有零点 内无零点
内无零点 内有零点
内有零点  内不一定有零点
内不一定有零点 上的奇函数
上的奇函数 满足
满足 ,且在区间
,且在区间 上是增函数.若方程
上是增函数.若方程 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ______
______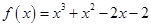 的一个正实数零点,其参考数据如下:
的一个正实数零点,其参考数据如下: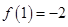


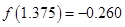

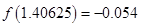
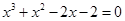 的一个近似根(精确到0.1)为 ( )
的一个近似根(精确到0.1)为 ( )  ( )
( ) 的图像与
的图像与 轴没有公共点,则m的取值范围是__________(用区间表示)。
轴没有公共点,则m的取值范围是__________(用区间表示)。