题目内容
已知α为锐角，试探求sinα+cosα的取值范围.
思路分析：利用三角函数的定义将sinα、cosα表示出来，再利用x、y、r的关系求解.
解：设M(x,y)是角α的终边上异于原点的一点，则有
,
.
∵α为锐角，∴x＞0,y＞0.
∴sinα+cosα=
+
=
=
=
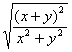
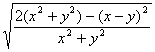
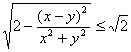（当且仅当x=y时取等号）.
又sinα+cosα=
+
=
=
=
.
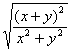
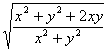
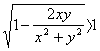综上,可知sinα+cosα的取值范围是(1, 
］.
练习册系列答案
相关题目
题目内容
已知α为锐角，试探求sinα+cosα的取值范围.
思路分析：利用三角函数的定义将sinα、cosα表示出来，再利用x、y、r的关系求解.
解：设M(x,y)是角α的终边上异于原点的一点，则有,
.
∵α为锐角，∴x＞0,y＞0.
∴sinα+cosα=+=
=
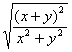
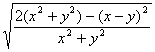
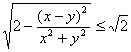=（当且仅当x=y时取等号）.
又sinα+cosα=+=
=
=.
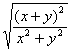
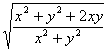
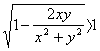综上,可知sinα+cosα的取值范围是(1, ］.