题目内容
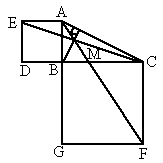
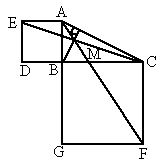
如图，以Rt△ABC的两条直角边AB、BC向形外作正方形ABDE和正方形BCFG，连结EC、AF交于M，求证：BM⊥AC．
答案：略
解析：
解析：
|
证明：如图，以两条直角边所在直线为坐标轴，建立直角坐标系，设正方形 ABCD和正方形BCFG的边长分别为a、b(a、b＞)，则A(0，a)，C(b，0)，B(0，0)，E(－a，a)，F(b，－b)．
由两点工得直线 AF和EC所在的直线方程分别为：AF ： ，即
EF ： ，即 ．
由 
解得： 
即 M点坐标为 ．
由于  ，
且  ，
即  ，
∴BM⊥AC ．建立适当的直角坐标系，将证明 BM⊥AC转化计算 ，也就是将几何证明转化为代数计算． |
练习册系列答案
出彩同步大试卷系列答案
相关题目
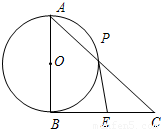
如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．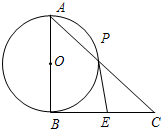
选修4-1：几何证明选讲
