题目内容
设函数 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为M上的
为M上的 高调函数,如果定义域为
高调函数,如果定义域为 的函数
的函数 为
为 上的
上的 高调函数,那么实数
高调函数,那么实数 的取值范围是_____________.
的取值范围是_____________.

解析试题分析:因为函数f(x)=x2在[-1,0]上为减函数,在[0,+∞)上是增函数,若满足函数f(x)=x2为[-1,+∞)上“n高调函数”,如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上k高调函数,只有[-1,1]上至少需要加2,那么实数k的取值范围是[2,+∞),
考点:函数单调性
点评:此题属于新定义的题型,涉及的知识有:函数单调性的判断与证明,以及基本初等函数的性质,其中认真审题,弄清新定义的本质,找到判断的标准是解本题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,若对给定的正数K,定义
,若对给定的正数K,定义 则当函数
则当函数 时,
时, 
 的值域是__________.
的值域是__________. 的定义域为 .
的定义域为 . (x≤-1),则f-1(2)= .
(x≤-1),则f-1(2)= . 的定义域为
的定义域为  =8,点
=8,点 在线段
在线段 =2,
=2, 为线段
为线段 上一动点,点
上一动点,点 绕点
绕点 绕点
绕点 .设
.设 =
= ,
, 
 的面积为
的面积为 .则
.则 的零点是 .
的零点是 . 
 △
△ =
= ,其中
,其中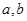 为正实数,若1△
为正实数,若1△ =3,则函数
=3,则函数 △
△ 的值域是 .
的值域是 . 的值域是
的值域是 ;
;