题目内容
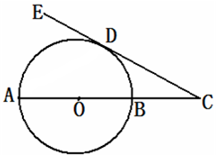 (2012•蓝山县模拟)如图,AB是⊙O的直径,直线DE切⊙O于点D,且与AB的延长线交于点C,若CD=
(2012•蓝山县模拟)如图,AB是⊙O的直径,直线DE切⊙O于点D,且与AB的延长线交于点C,若CD=| 3 |
30°
30°
.分析:利用切割线定理,先计算出圆的半径,再利用直角三角形中的三角函数,即可求得结论.
解答:解:∵直线DE切⊙O于点D,且与AB的延长线交于点C
∴CD2=CB×CA
∵CD=
,CB=1,
∴CA=3
∴AB=2
∴OD=1
连接OD,则OD⊥CD,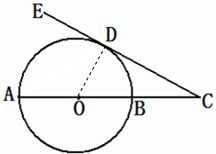
在直角三角形OCD中,OD=1,OC=2,∴sin∠OCD=
=
∴∠OCD=30°
即∠ACE=30°
故答案为:30°
∴CD2=CB×CA
∵CD=
| 3 |
∴CA=3
∴AB=2
∴OD=1
连接OD,则OD⊥CD,

在直角三角形OCD中,OD=1,OC=2,∴sin∠OCD=
| OD |
| OC |
| 1 |
| 2 |
∴∠OCD=30°
即∠ACE=30°
故答案为:30°
点评:本题考查圆的切线的性质,考查切割线定理,考查三角函数,属于中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目