题目内容
已知函数 ,
, .
.
(1)求 的值;
的值;
(2)求f(x)的单调区间;
(3)若不等式|f(x)-m|<2恒成立,求实数m的取值范围.
解:(1) .
.
(2) =
= .
.
又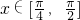 ,
,
∴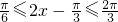 ,
,
当 时,f(x)单调递增;
时,f(x)单调递增;
当 时,f(x)单调递减,
时,f(x)单调递减,
所以f(x)的单调递增区间是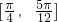 ;
;
f(x)的单调递减区间是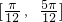 .
.
(3)由(2)得 ,
,
∴f(x)的值域是[2,3].
|f(x)-m|<2?f(x)-2<m<f(x)+2,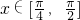 .
.
∴m>f(x)max-2且 m<f(x)min+2,
∴1<m<4,即m的取值范围是(1,4).
分析:(1)根据所给的解析式,代入所给的自变量的值,计算出结果,本题也可以先化简再代入数值进行运算.
(2)把所给的三角函数的解析式进行恒等变形,整理出y=Asin(ωx+φ)的形式,根据正弦曲线的单调性写出ωx+φ所在的区间,解出不等式即可.
(3)根据前面整理出来的结果,得到f(x)的值域,不等式|f(x)-m|<2恒成立,解出关于绝对值的不等式,求出结果.
点评:本题考查三角函数的恒等变换和三角函数的最值,本题解题的关键是正确整理出函数的最简结果,本题的难度和高考卷中出现的题目的难度相似.
 .
. (2)
 =
= .
. 又
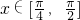 ,
,∴
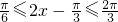 ,
,当
 时,f(x)单调递增;
时,f(x)单调递增;当
 时,f(x)单调递减,
时,f(x)单调递减,所以f(x)的单调递增区间是
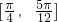 ;
;f(x)的单调递减区间是
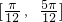 .
. (3)由(2)得
 ,
,∴f(x)的值域是[2,3].
|f(x)-m|<2?f(x)-2<m<f(x)+2,
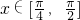 .
.∴m>f(x)max-2且 m<f(x)min+2,
∴1<m<4,即m的取值范围是(1,4).
分析:(1)根据所给的解析式,代入所给的自变量的值,计算出结果,本题也可以先化简再代入数值进行运算.
(2)把所给的三角函数的解析式进行恒等变形,整理出y=Asin(ωx+φ)的形式,根据正弦曲线的单调性写出ωx+φ所在的区间,解出不等式即可.
(3)根据前面整理出来的结果,得到f(x)的值域,不等式|f(x)-m|<2恒成立,解出关于绝对值的不等式,求出结果.
点评:本题考查三角函数的恒等变换和三角函数的最值,本题解题的关键是正确整理出函数的最简结果,本题的难度和高考卷中出现的题目的难度相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目