题目内容
函数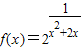
的值域为 ．
【答案】分析：先求出f（x）的定义域，再利用指数函数的性质，对定义域进行讨论，求出f（x）的值域；
解答：解：∵函数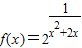
，
∴f（x）的定义域{x|x≠0且x≠-2}，
若x＞0，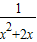
＞0，
因为x2+2x=（x+1）2-1≥0，所以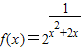
＞2=1；
若-2＜x＜0时，
∵x2+2x=（x+1）2-1，∴-1≤x2+2x＜0，
∴
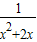≤-1，∴
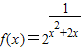≤2-1=
，
因为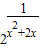
＞0，∴0＜f（x）≤
，
若x＜-2，x2+2x＞0，可得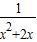
＞0，可得f（x）＞2=1，
综上：f（x）∈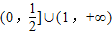
；
故答案为：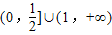
点评：此题主要指数函数的性质，是一道基础题，解题的过程中用到了分类讨论的思想，也是一道好题；
解答：解：∵函数
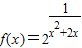，∴f（x）的定义域{x|x≠0且x≠-2}，
若x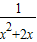＞0，
＞0，因为x2+2x=（x+1）2-1≥0，所以
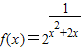＞2=1；若-2＜x＜0时，
∵x2+2x=（x+1）2-1，∴-1≤x2+2x＜0，
∴
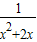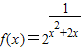≤-1，∴≤2-1=，因为
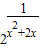＞0，∴0＜f（x）≤，若x＜-2，x2+2x＞0，可得
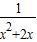＞0，可得f（x）＞2=1，综上：f（x）∈
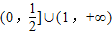；故答案为：
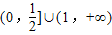
点评：此题主要指数函数的性质，是一道基础题，解题的过程中用到了分类讨论的思想，也是一道好题；
练习册系列答案
相关题目
读图分析解答：设定义在闭区间[-4，4]上的函数y=f（x）的图象如图所示（图中坐标点都是实心点），完成以下几个问题：