题目内容
函数f(x)=lnx,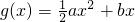 (a≠0)
(a≠0)
(1)b=2时,函数h(x)=f(x)-g(x)存在减区间,求a的取值范围
(2)函数f(x)的图象与函数g(x)的图象交于P,Q两点,过PQ中点作x轴的垂线l,l与曲线y=f(x),y=g(x)分别交于M,N点,设曲线y=f(x)在M处的切线为l1,曲线y=g(x)在N处的切线为l2,证明l1∥l2.
解:(1)当b=2时,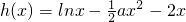 ,
,
函数h(x)=f(x)-g(x)存在减区间,等价于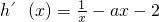 <0,在x>0时解集非空集,
<0,在x>0时解集非空集,
即关于x的不等式ax2+2x-1>0(a≠0)有解,
当a>0时,ax2+2x-1>0显然有解;
而当a<0时,只需△=4+4a>0,解得-1<a<0,
∴a的取值范围为:a>0或-1<a<0 …(7分)
(2)设P(x1,y1),Q(x2,y2),设0<x1<x2,由题意可得M、N的横坐标 ,
,
则M点处的导数值为 ,N点处的导数值为
,N点处的导数值为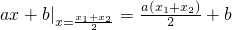 ,
,
假设存在0<x1<x2使l1∥l2,即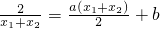 ,
,
∴ =
= =f(x1)-f(x2)=
=f(x1)-f(x2)=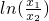 ,
,
假设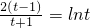 (*),
(*),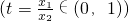 …(10分)
…(10分)
考虑 t∈(0,1)的单调性,
t∈(0,1)的单调性,
∵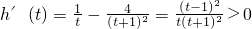
可知h(t)是t∈(0,1)的增函数(也是R+上增函数),故h(t)<h(1)=0,
因此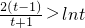 ,
,
此结论与题设(*)矛盾,
∴l1∥l2…(14分)
分析:(1)把b=2代入可得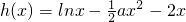 ,而函数h(x)=f(x)-g(x)存在减区间等价于
,而函数h(x)=f(x)-g(x)存在减区间等价于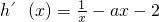 <0在x>0时解集非空集,分类讨论可得;
<0在x>0时解集非空集,分类讨论可得;
(2)假设存在0<x1<x2使l1∥l2,即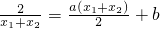 ,从而有
,从而有 =
=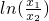 ,由导数法考虑
,由导数法考虑 t∈(0,1)的单调性可得.
t∈(0,1)的单调性可得.
点评:本题考查函数与导数的综合应用,涉及函数的恒成立问题以及构造函数利用单调性证明问题,属中档题.
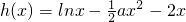 ,
,函数h(x)=f(x)-g(x)存在减区间,等价于
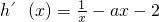 <0,在x>0时解集非空集,
<0,在x>0时解集非空集,即关于x的不等式ax2+2x-1>0(a≠0)有解,
当a>0时,ax2+2x-1>0显然有解;
而当a<0时,只需△=4+4a>0,解得-1<a<0,
∴a的取值范围为:a>0或-1<a<0 …(7分)
(2)设P(x1,y1),Q(x2,y2),设0<x1<x2,由题意可得M、N的横坐标
 ,
,则M点处的导数值为
 ,N点处的导数值为
,N点处的导数值为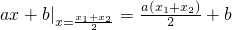 ,
,假设存在0<x1<x2使l1∥l2,即
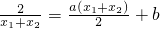 ,
,∴
 =
= =f(x1)-f(x2)=
=f(x1)-f(x2)=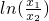 ,
,假设
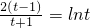 (*),
(*),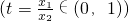 …(10分)
…(10分)考虑
 t∈(0,1)的单调性,
t∈(0,1)的单调性,∵
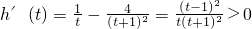
可知h(t)是t∈(0,1)的增函数(也是R+上增函数),故h(t)<h(1)=0,
因此
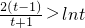 ,
,此结论与题设(*)矛盾,
∴l1∥l2…(14分)
分析:(1)把b=2代入可得
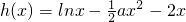 ,而函数h(x)=f(x)-g(x)存在减区间等价于
,而函数h(x)=f(x)-g(x)存在减区间等价于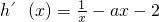 <0在x>0时解集非空集,分类讨论可得;
<0在x>0时解集非空集,分类讨论可得;(2)假设存在0<x1<x2使l1∥l2,即
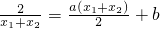 ,从而有
,从而有 =
=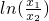 ,由导数法考虑
,由导数法考虑 t∈(0,1)的单调性可得.
t∈(0,1)的单调性可得.点评:本题考查函数与导数的综合应用,涉及函数的恒成立问题以及构造函数利用单调性证明问题,属中档题.

练习册系列答案
相关题目