题目内容
已知关于x的一元二次不等式ax2+bx+c≥0在实数集上恒成立,且a<b,则 的最小值为________.
的最小值为________.
3
分析:从二次函数的二次项系数及判别式限制,得到a,b,c满足的不等关系;将M中的c利用得到的不等关系去掉;将代数式变形,利用基本不等式求出最小值,
解答:∵一元二次不等式ax2+bxx+c≥0对一切实数x都成立,
当a=0时,不符合题意;
当a≠0时,根据y=ax2+bxx+c的图象
∴ ,由此
,由此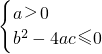
∵b>a>0∴b-a>0
∵b2≤4ac得c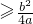
则 ≥
≥ =
=

 即c=b=4a时,取等号
即c=b=4a时,取等号
故答案为3
点评:主要考查了二次函数的恒成立问题.二次函数的恒成立问题分两类,一是大于0恒成立须满足开口向上,且判别式小于0,二是小于0恒成立须满足开口向下,且判别式小于0.
分析:从二次函数的二次项系数及判别式限制,得到a,b,c满足的不等关系;将M中的c利用得到的不等关系去掉;将代数式变形,利用基本不等式求出最小值,
解答:∵一元二次不等式ax2+bxx+c≥0对一切实数x都成立,
当a=0时,不符合题意;
当a≠0时,根据y=ax2+bxx+c的图象
∴
 ,由此
,由此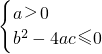
∵b>a>0∴b-a>0
∵b2≤4ac得c
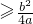
则
 ≥
≥ =
=

 即c=b=4a时,取等号
即c=b=4a时,取等号故答案为3
点评:主要考查了二次函数的恒成立问题.二次函数的恒成立问题分两类,一是大于0恒成立须满足开口向上,且判别式小于0,二是小于0恒成立须满足开口向下,且判别式小于0.

练习册系列答案
相关题目