题目内容
在下列各题中,请作出判断并说明理由.(1)p:x2-2x-3<0,q:|x|>3,则p是q的什么条件;
(2)p:m<-2;q:x2-x-m=0无实根,则q是p的什么条件;
(3)p:平行四边形,q:正方形,则q是p的什么条件;
(4)p:x>0,q:x≥5,则p是q的什么条件.
解:用集合法来判断:令A={x|p(x)},B={x|q(x)}.
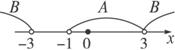
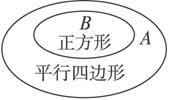
图1 图2
(1)设A={x|x2-2x-3<0}={x|-1<x<3},B={x||x|>3}={x|x>3或x<-3}.由图1可知A![]() B,且B
B,且B![]() A,∴p是q的既非充分也非必要条件.
A,∴p是q的既非充分也非必要条件.
(2)A={m|m<-2},B={m|Δ=1+4m<0}={m|m<-![]() },∴A
},∴A![]() B.
B.
故q是p必要不充分条件.
(3)设A={平行四边形},B={正方形},由图2可知B![]() A,∴q是p的充分不必要条件.
A,∴q是p的充分不必要条件.
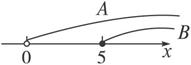
图3
(4)设A={x|x>0},B={x|x≥5},由图3可知B![]() A,∴p是q的必要不充分条件.
A,∴p是q的必要不充分条件.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目