题目内容
某地区举办青少年科技创新大赛,有50件科技创新作品进入了最后的评审阶段,大赛组委会对这50件作品分别从“艺术与创新”和“功能与实用”两项进行评分,每项评分均按等级采用5分制,若设“艺术与创新”得分为x,“功能与实用”得分为y,统计结果如下表: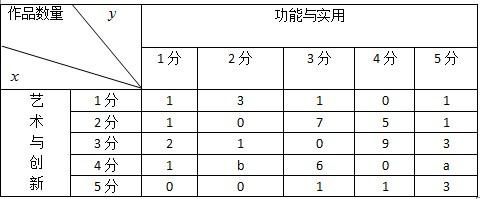
(Ⅰ)求“艺术与创新为4分且功能与实用为3分”的概率;
(Ⅱ)若“功能与实用”得分的数学期望为
| 167 | 50 |
分析:(Ⅰ)求“艺术与创新为4分且功能与实用为3分”的概率,可以根据图表看出“艺术与创新为4分且功能与实用为3分”有6件作品,除以总的作品数即可得到答案.
(Ⅱ)若“功能与实用”得分的数学期望为
,求a、b的值.因为由作品的总数可以求得a+b=3,又由表可知“功能与实用”得分y有1分、2分、3分、4分、5分五个等级,分别求出每个等级的概率,即可得到分布列,再根据期望公式求得期望即可,有2个含有a,b的表达式即可解出答案.
(Ⅱ)若“功能与实用”得分的数学期望为
| 167 |
| 50 |
解答:解:∵作品数量共有50件,∴可以求得:a+b=3①
(Ⅰ)从表中可以看出,“艺术与创新为4分且功能与实用为3分”的作品数量为6件,
∴“艺术与创新为4分且功能与实用为3分”的概率为
=0.12.
(Ⅱ)由表可知“功能与实用”得分y有1分、2分、3分、4分、5分五个等级,
且每个等级分别有5件,b+4件,15件,15件,a+8件.
∴“功能与实用”得分y的分布列为:

又∵“功能与实用”得分的数学期望为
,
∴1×
+2×
+3×
+4×
+5×
=
与①式联立可解得:a=1,b=2.
即答案为a=1,b=2.
(Ⅰ)从表中可以看出,“艺术与创新为4分且功能与实用为3分”的作品数量为6件,
∴“艺术与创新为4分且功能与实用为3分”的概率为
| 6 |
| 50 |
(Ⅱ)由表可知“功能与实用”得分y有1分、2分、3分、4分、5分五个等级,
且每个等级分别有5件,b+4件,15件,15件,a+8件.
∴“功能与实用”得分y的分布列为:

又∵“功能与实用”得分的数学期望为
| 167 |
| 50 |
∴1×
| 5 |
| 50 |
| b+4 |
| 50 |
| 15 |
| 50 |
| 15 |
| 50 |
| a+8 |
| 50 |
| 167 |
| 50 |
与①式联立可解得:a=1,b=2.
即答案为a=1,b=2.
点评:此题主要考查离散型随机变量的分布列和期望的求法,对于此类图表型的题目仔细分析图表是题目的关键,切记不可偏离图表.同学们需要注意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,求a、b的值.
,求a、b的值.
 ,求a,b的值。
,求a,b的值。 
 ,求a、b的值.
,求a、b的值.