题目内容
设全集为U=R,集合A为函数f(x)=
+lg(3-x)-1的定义域,B={x|2x-4≥x-2}
(1)求A∪B,?U(A∩B)
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
| x+1 |
(1)求A∪B,?U(A∩B)
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
(1)解不等式组
,得-1≤x<3,
∴f(x)=
+lg(3-x)-1的定义域A=[-1,3),
又∵集合B={x|2x-4≥x-2}=[2,+∞),
∴A∩B=[2,3),A∪B=[-1,+∞),
∵全集为U=R,
∴?U(A∩B)=(-∞,2)∪[3,+∞),
综上所述,得A∪B=[-1,+∞),?U(A∩B)=(-∞,2)∪[3,+∞).
(2)由(1)得集合B=[2,+∞),
∵C={x|2x+a>0}=(-
,+∞),且B∪C=C,
∴B?C,可得-
<2,解之得a>-4.
即实数a的取值范围是(-4,+∞).
|
∴f(x)=
| x+1 |
又∵集合B={x|2x-4≥x-2}=[2,+∞),
∴A∩B=[2,3),A∪B=[-1,+∞),
∵全集为U=R,
∴?U(A∩B)=(-∞,2)∪[3,+∞),
综上所述,得A∪B=[-1,+∞),?U(A∩B)=(-∞,2)∪[3,+∞).
(2)由(1)得集合B=[2,+∞),
∵C={x|2x+a>0}=(-
| a |
| 2 |
∴B?C,可得-
| a |
| 2 |
即实数a的取值范围是(-4,+∞).

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 设全集为U=R,集合A={x|(x+3)(6-x)≤0},B={x|log2(x+2)<4}.
设全集为U=R,集合A={x|(x+3)(6-x)≤0},B={x|log2(x+2)<4}. 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|log2(x+2)<4}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|log2(x+2)<4}.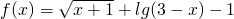 的定义域,B={x|2x-4≥x-2}
的定义域,B={x|2x-4≥x-2}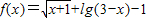 的定义域,B={x|2x-4≥x-2}
的定义域,B={x|2x-4≥x-2}