��Ŀ����
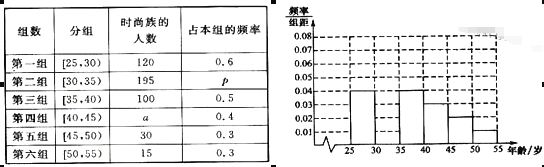
����Ŀ��ij�������Ž������ʵ������![]() �����Ⱥ�����ȡn�˽�����һ���Ƿ�ͨ�������ĵ��飬����ͨ�������ij�Ϊ��ʱ���塱�������Ϊ����ʱ���塱��ͨ������ֱ�õ���ͼ��ʾͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�����Ⱥ�����ȡn�˽�����һ���Ƿ�ͨ�������ĵ��飬����ͨ�������ij�Ϊ��ʱ���塱�������Ϊ����ʱ���塱��ͨ������ֱ�õ���ͼ��ʾͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
����������⣺
����ȫƵ�ʷֲ�ֱ��ͼ����![]() ��ֵ��
��ֵ��
����![]() ������εġ�ʱ���塱�в��÷ֲ��������ȡ
������εġ�ʱ���塱�в��÷ֲ��������ȡ![]() �˲μ�����ʱ�д��˴���������ѡȡ
�˲μ�����ʱ�д��˴���������ѡȡ![]() ����Ϊ��ӣ���ѡȡ��
����Ϊ��ӣ���ѡȡ��![]() �������������
�������������![]() �������Ϊ
�������Ϊ![]() ����
����![]() �ķֲ���
�ķֲ���
���𰸡���Ƶ�ʷֲ�ͼ�ԣ�![]() ��
��![]() ��
��![]() ���Ƽ�����
���Ƽ�����
��������
������������ε������Ϊ1����ڶ����Ƶ�ʣ�Ȼ������ߣ�����Ƶ��ֱ��ͼ�������һ���������Ƶ�ʴӶ����n�������֪���ڶ����Ƶ���Լ��������Ӷ����p��ֵ��Ȼ������������Ƶ�ʺ������Ӷ����a��ֵ��
������Ϊ[40��45��������εġ�ʱ���塱��[45��50��������εġ�ʱ���塱�ı�ֵΪ2��1�����Բ��÷ֲ��������ȡ18�ˣ�[40��45��������12�ˣ�[45��50��������6�ˣ�������X���ӳ����ηֲ���X��ȡֵ����Ϊ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��г��ֲ��У�
���ڶ����Ƶ��Ϊ![]() ��
��
���Ը�Ϊ![]() ��Ƶ��ֱ��ͼ���£�
��Ƶ��ֱ��ͼ���£�

��һ�������Ϊ![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ������
������![]()
�����֪���ڶ����Ƶ��Ϊ![]() �����Եڶ��������Ϊ
�����Եڶ��������Ϊ![]() ��
��
����![]() ��
��
�������Ƶ��Ϊ![]() �����Ե����������Ϊ
�����Ե����������Ϊ![]() ��
��
����![]()
����Ϊ[40��45��������εġ�ʱ���塱��[45��50��������εġ�ʱ���塱�ı�ֵ
Ϊ![]() ��
��
���Բ��÷ֲ��������ȡ18�ˣ�[40��45��������12�ˣ�[45��50��������6�ˣ�
�������![]() ���ӳ����ηֲ�
���ӳ����ηֲ�
![]() ��
��![]() ��
��![]()
![]() ,
,
�����������X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|

����Ŀ������������һλ���۾����ռ�����ÿ�����۶�y(ǧԪ)�����۾���x(��)�Ĺ�ϵ��
���۾���x/�� | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
�����۶�y/ǧԪ | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)������Щ���ݻ���ɢ��ͼ����ֱ��![]() ��78��4.2x������
��78��4.2x������![]() ��
��
(2)������Щ������ع�ֱ�߷��̲��ݴ˼���![]() ��
��
(3)�Ƚ�(1) (2)�еIJв�ƽ����![]() �Ĵ�С.
�Ĵ�С.
