题目内容
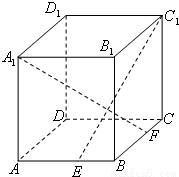
如图,ABCD-A1B1C1D1是正方体,E、F分别是AD、DD1的中点,则面EFC1B和面BCC1所成二面角的正切值等于
C
解析:
为了作出二面角E-BC1-C的平面角,需在一个面内取一点,过该点向另一个面引垂线(这是用三垂线定理作二面角的平面角的关键步骤)。
从图形特点看,应当过E(或F)作面BCC1的垂线.过E作EH⊥BC,垂足为H. 过H作HG⊥BC1,垂足为G.连EG.
∵面ABCD⊥面BCC1,而EH⊥BC
∵EH⊥面BEC1,
EG是面BCC1的斜线,HG是斜线EG在面BCC1内的射影.
∵HG⊥BC1, 
∴EG⊥BC1,
∴∠EGH是二面角E-BC1-C的平面角。
在Rt△BCC1中:sin∠C1BC=![]() =
=![]()
在Rt△BHG中:sin∠C1BC=![]()
∴HG=![]() (设底面边长为1).
(设底面边长为1).
而EH=1,
在Rt△EHG中:tg∠EGH=![]()
∴∠EGH=arctg![]()
故二面角E-BC1-C 等于arctg![]() .
. 

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
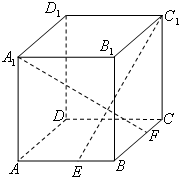 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是