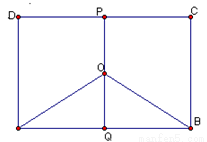
题目内容
某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km, ![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式。
的函数关系式。
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短。

(I)①![]()
②![]()
(Ⅱ)选择函数模型①,P位于线段AB的中垂线上且距离AB边![]() 处。
处。
解析:
本小题考查函数最值的应用。
(I)①由条件可知PQ垂直平分AB,![]() ,则
,则![]()
故![]() ,又
,又![]() ,所以
,所以
![]()
![]() 。
。
②![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以所求的函数关系式为![]() 。
。
(Ⅱ)选择函数模型①。
![]() 。
。
令![]() 得
得![]() ,又
,又![]() ,所以
,所以![]() 。
。
当![]() 时,
时,![]() ,
,![]() 是
是![]() 的减函数;
的减函数;![]() 时,
时,![]() ,
,![]() 是
是![]() 的增函数。
的增函数。
所以当![]() 时
时![]() 。当P位于线段AB的中垂线上且距离AB边
。当P位于线段AB的中垂线上且距离AB边![]() 处。
处。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=20km,BC=10km.为了处理这三家工厂的污水,现要在该矩形区域上(含边界)且与A,B等距的一点O处,建造一个污水处理厂,并铺设三条排污管道AO,BO,PO.记铺设管道的总长度为ykm.
如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=20km,BC=10km.为了处理这三家工厂的污水,现要在该矩形区域上(含边界)且与A,B等距的一点O处,建造一个污水处理厂,并铺设三条排污管道AO,BO,PO.记铺设管道的总长度为ykm.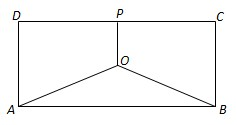 某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm.
某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm. (I)按下列要求写出函数关系式:
(I)按下列要求写出函数关系式: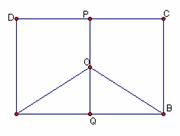
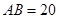 km,
km, 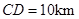 ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。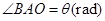 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;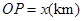 ,将
,将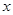 的函数关系式。
的函数关系式。