题目内容
8.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2+1,值域为{3,9}的“孪生函数”共有( )| A. | 1个 | B. | 3个 | C. | 7个 | D. | 9个 |
分析 根据“孪生函数”的定义确定函数定义域的不同即可.
解答 解:由y=2x2+1=3,得x2=1,即x=1或x=-1,
由y=2x2+1=9,得x2=4,即x=2或x=-2,
即定义域内-1和1至少有一个,有3种结果,
-2和2至少有一个,有3种结果,
∴共有3×3=9种,
故选:D.
点评 本题主要考查函数定义域和值域的求法,利用“孪生函数”的定义是解决本题的关键.

练习册系列答案
相关题目
16.已知离心率为$\frac{1}{2}$的椭圆的左右焦点分别为F1,F2,椭圆上一点P满足:|PF1|=2|PF2|,则cos∠PF1F2=( )
| A. | $\frac{11}{16}$ | B. | $\frac{7}{8}$ | C. | -$\frac{1}{4}$ | D. | 不确定 |
13.若曲线y=xα+1(α∈R)在(1,2)处的切线经过原点,则α=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.若f(x)=sinx+cosx,f′(x)是f(x)的导函数,要得到g(x)=$\sqrt{2}f(x){f}^{′}$(x)的图象,需将f(2x)的图象( )
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向右平移 $\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
 如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$.
如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$.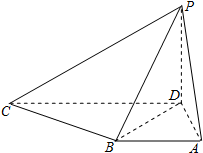 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.