题目内容
统计某产品的广告费用x与销售额y的一组数据如下表:
广告费用 | 2 | 3 | 5 | 6 |
销售额 | 7 |  | 9 | 12 |
 对
对 的回归直线方程是
的回归直线方程是 ,则数据中的
,则数据中的 的值应该是( )
的值应该是( )A.7.9 B.8 C.8.1 D.9
B
解析试题分析:因为用最小二乘法可求得 对
对 的回归直线方程是
的回归直线方程是 ,则说明b=1,1,a=4.6,由于线性回归方程必定过样本中心点
,则说明b=1,1,a=4.6,由于线性回归方程必定过样本中心点 ,且有
,且有 ,而根据表格得到4
,而根据表格得到4 =2+3+5+6,
=2+3+5+6, =4;代入上式中可知,
=4;代入上式中可知, ,4
,4 =7+m+9+12,m=8,选B.
=7+m+9+12,m=8,选B.
考点:本试题主要考查了线性回归方程中系数之间的关系的运用。
点评:解决该试题的关键是理解 中a,b分别是谁。
中a,b分别是谁。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
一组数据中,每一个数都减去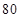 ,得到一组新数据,若求得新数据的平均数是
,得到一组新数据,若求得新数据的平均数是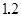 ,方差是
,方差是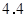 ,则原来数据的平均数和方差分别为( )
,则原来数据的平均数和方差分别为( )
A.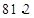 , , 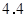 | B.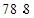 , , 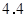 | C.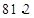 , , 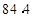 | D.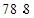 , ,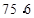 |
某地区教育主管部门为了对该地区模拟考试成绩进行分析,抽取了总成绩介于350分到650分之间的10000名学生成绩,并根据这10000名学生的总成绩画了样本的频率分布直方图(如右图),则总成绩在[400,500)内共有( )
| A.5000 人 | B.4500人 |
| C.3250人 | D.2500人 |
右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,中间的数字表示得分的十位数,下列对乙运动员的判断错误的是 ( )
| A.乙运动员得分的中位数是28 |
| B.乙运动员得分的众数为31 |
| C.乙运动员的场均得分高于甲运动员 |
| D.乙运动员的最低得分为0分 |

已知一组数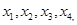 的平均数是
的平均数是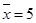 ,方差
,方差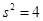 ,则数据
,则数据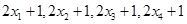 的平均数和方差分别是( )
的平均数和方差分别是( )
| A.11,8 | B.10,8 | C.11,16 | D.10,16 |
某学校为了了解高一年级学生对教师教学的意见,打算从高一年级2007名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从2007人中剔除7人,剩下2000人再按系统抽样的方法进行,则每人入选的机会( )
| A.不全相等 | B.均不相等 | C.无法确定 | D.都相等 |
有关线性回归的说法,不正确的是( )
| A.相关关系的两个变量不是因果关系 |
| B.散点图能直观地反映数据的相关程度 |
| C.回归直线最能代表线性相关的两个变量之间的关系 |
| D.任一组数据都有回归方程 |
甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验,并用回归分析方法分别求得相关系数r与残差平方和m如下表;则哪位同学的试验结果体现A、B两变量更强的线性相关性
A.丁 B.丙 C.乙 D.甲
| | 甲 | 乙 | 丙 | 丁 |
| r | 0.82 | 0.78 | 0.69 | 0.85 |
| m | 115 | 106 | 124 | 103 |