题目内容
设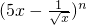 的展开式的各项系数和为M,二项式系数和为N,若M-N=240,则展开式中x的系数为
的展开式的各项系数和为M,二项式系数和为N,若M-N=240,则展开式中x的系数为
- A.-150
- B.150
- C.300
- D.-300
B
分析:由题意可得4n-2n=240,求得n值,确定通项,令x的指数为1,即可求得结论.
解答:由题意可得 4n-2n=240,∴n=4.
通项Tr+1=C4r (5x)4-r (-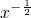 )r=(-1)r C4r 54-r
)r=(-1)r C4r 54-r  ,
,
令4- r=1,可得r=2
r=1,可得r=2
∴展开式中x的系数为(-1)2 C42 52=150
故选B.
点评:本题考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,求出 r=2,是解题的关键.
分析:由题意可得4n-2n=240,求得n值,确定通项,令x的指数为1,即可求得结论.
解答:由题意可得 4n-2n=240,∴n=4.
通项Tr+1=C4r (5x)4-r (-
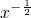 )r=(-1)r C4r 54-r
)r=(-1)r C4r 54-r  ,
,令4-
 r=1,可得r=2
r=1,可得r=2∴展开式中x的系数为(-1)2 C42 52=150
故选B.
点评:本题考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,求出 r=2,是解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 的展开式的各项系数之和为
的展开式的各项系数之和为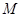 ,二项式系数之和为
,二项式系数之和为 ,若
,若 ,则展开式中常数项为___________.
,则展开式中常数项为___________. 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
)
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
) 的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____
的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____ 的展开式的各项系数之和为M,二项式系数之和为N,若
的展开式的各项系数之和为M,二项式系数之和为N,若 ,则展开式中
,则展开式中 的系数为 。
的系数为 。 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )