题目内容
设数列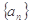 的前
的前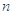 项和为
项和为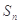 ,对一切
,对一切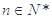 ,点
,点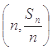 都在函数
都在函数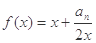 的图象上
的图象上
(1)求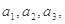 归纳数列
归纳数列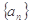 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列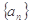 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(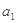 ),
),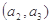 ,
,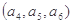 ,
,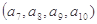 ;
;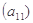 ,
,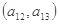 ,
,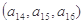 ,
,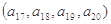 ;
;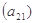 ,…..,
,…..,
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为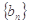 ,
,
求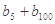 的值;
的值;
(3)设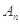 为数列
为数列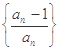 的前
的前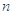 项积,若不等式
项积,若不等式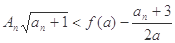 对一切
对一切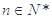 都成立,其中
都成立,其中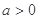 ,求
,求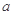 的取值范围
的取值范围
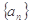 的前
的前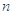 项和为
项和为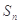 ,对一切
,对一切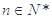 ,点
,点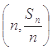 都在函数
都在函数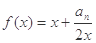 的图象上
的图象上(1)求
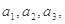 归纳数列
归纳数列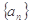 的通项公式(不必证明);
的通项公式(不必证明);(2)将数列
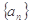 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为(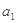 ),
),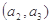 ,
,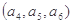 ,
,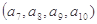 ;
;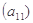 ,
,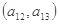 ,
,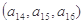 ,
,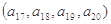 ;
;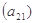 ,…..,
,…..,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
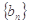 ,
,求
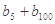 的值;
的值;(3)设
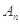 为数列
为数列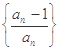 的前
的前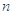 项积,若不等式
项积,若不等式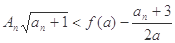 对一切
对一切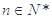 都成立,其中
都成立,其中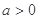 ,求
,求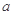 的取值范围
的取值范围(1)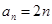 ;(2)2010;(3)
;(2)2010;(3)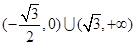
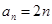 ;(2)2010;(3)
;(2)2010;(3)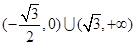
试题分析:(1)根据题意求处前几项
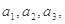 ,利用归纳推理猜想通项公式
,利用归纳推理猜想通项公式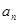 ;(2)观察发现规律,可得:
;(2)观察发现规律,可得: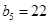 ,
,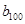 是第25组中第4个括号内各数之和;(3)将恒成立问题转化为求函数的最值进行求解.
是第25组中第4个括号内各数之和;(3)将恒成立问题转化为求函数的最值进行求解.规律总结:1.归纳推理是合情推理的一种,对数学定理、结论的求解起到非常重要的作用;此类题型的关键是通过已知的项,发现内在的规律与联系,进而提出猜想;2.求序号较大的项时,往往要探索是否具有周期性;3.对于不等式的恒成立问题,主要思路是将所求参数进行分离,将其转化为求函数的最值问题.
试题解析:(1)因为点
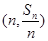 在函数
在函数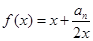 的图象上,
的图象上,故
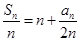 ,所以
,所以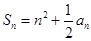 .
.令
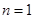 ,得
,得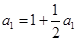 ,所以
,所以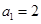 ;
;令
 ,得
,得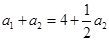 ,所以
,所以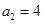 ;
;令
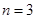 ,得
,得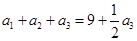 ,所以
,所以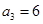 .
.由此猜想:
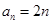
(2)因为
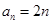 (
(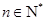 ),所以数列
),所以数列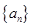 依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循环记为一组.由于每一个循环含有4个括号, 故
依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),…. 每一次循环记为一组.由于每一个循环含有4个括号, 故 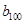 是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20. 同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20. 故各组第4个括号中各数之和构成等差数列,且公差为80. 注意到第一组中第4个括号内各数之和是68,
是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20. 同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20. 故各组第4个括号中各数之和构成等差数列,且公差为80. 注意到第一组中第4个括号内各数之和是68,所以
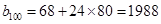 .又
.又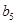 =22,所以
=22,所以 =2010.
=2010.(3)因为
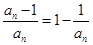 ,故
,故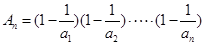 ,
,所以
 .
.又
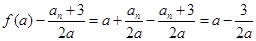 ,
,故
 对一切
对一切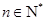 都成立,就是
都成立,就是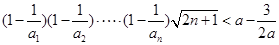 对一切
对一切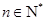 都成立
都成立设
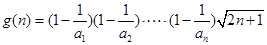 ,则只需
,则只需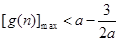 即可.
即可.由于
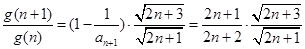
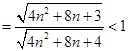 ,
,所以
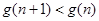 ,故
,故 是单调递减,于是
是单调递减,于是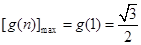 .
.令
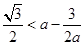 ,
,即
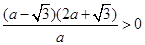 ,解得
,解得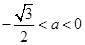 ,或
,或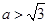 .
.综上所述,使得所给不等式对一切
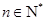 都成立的实数
都成立的实数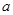 的取值范围是
的取值范围是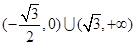 .
.
练习册系列答案
相关题目
 的首项
的首项 ,前
,前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列,其中
成等差数列,其中 .
. 满足:
满足: ,记数列
,记数列 ,求
,求 的最大项.
的最大项. .
. 为等差数列,且
为等差数列,且 ,则公差
,则公差 = .
= . ,则
,则 的值为( ).
的值为( ).



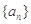 的通项公式
的通项公式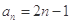 ,设数列
,设数列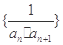 ,其前n项和为
,其前n项和为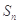 ,则
,则

