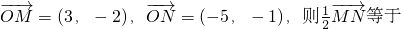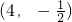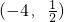Question

已知向量a=（8，

1

2

x，x）．b=（x，1，2），其中x＞0．若a∥b，则x的值为（　　）

• A、8
• B、4
• C、2
• D、0

Answer 1

分析：根据两个向量平行，写出两个向量平行的充要条件，得到两个向量的坐标之间的关系，根据横标、纵标和竖标分别相等，得到λ和x的值．

解答：解：∵

a

∥

b

且x＞0
存在λ＞0使

a

=λ

b

∴（8，

1

2

x，x）=（λx，λ，2λ）
∴

λx=8 x 2 =λ x=2λ

∴

λ=2 x=4

．
故选B

点评：本题考查共线向量的充要条件的应用，是一个基础题，这种题目可以作为选择和填空出现在高考题目中，是一个送分题目．