题目内容
已知函数f(x)=ax2+2ln(1﹣x)(a∈R).
(1)若f(x)在x=﹣1处有极值,求a的值;
(2)若f(x)在[﹣3,﹣2)上是增函数,求实数a的取值范围;
(3)是否存在正实数a,使得f(x)的导函数f′(x)满足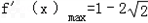 ,
,
若存在,求出a的值,若不存在说明理由.
(1)若f(x)在x=﹣1处有极值,求a的值;
(2)若f(x)在[﹣3,﹣2)上是增函数,求实数a的取值范围;
(3)是否存在正实数a,使得f(x)的导函数f′(x)满足
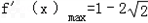 ,
,若存在,求出a的值,若不存在说明理由.
解:(1)∵f(x)=ax2+2ln(1﹣x),
∴1﹣x>0,即x<1,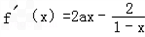 ,
,
∵f(x)在x=﹣1处有极值,
∴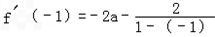 =0,
=0,
解得a=﹣ .
.
(2)∵f(x)在[﹣3,﹣2)上是增函数,
∴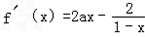 ≥0对一切x∈[﹣3,﹣2)恒成立,
≥0对一切x∈[﹣3,﹣2)恒成立,
∴a≤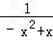 =
=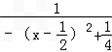 ,
,
当x∈[﹣3,﹣2)时,﹣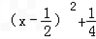 <﹣6,
<﹣6,
∴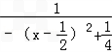 >﹣
>﹣ .
.
故a≤﹣ .
.
(3)假设存在正数a,使得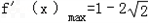 成立,
成立,
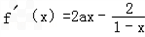 =2a﹣[2a(1﹣x)+
=2a﹣[2a(1﹣x)+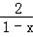 ]≤
]≤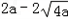 ,
,
由2a(1﹣x)=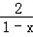 ,得(1﹣x)2=
,得(1﹣x)2= ,
,
∴x=1±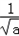 ,由于x=1+
,由于x=1+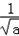 >1,故应舍去,
>1,故应舍去,
当x=1﹣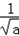 时,
时,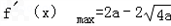 ,
,
令2a﹣2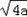 =1﹣2
=1﹣2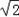 ,解得a=
,解得a= ,或a=
,或a=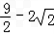 .
.
∴1﹣x>0,即x<1,
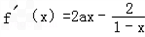 ,
,∵f(x)在x=﹣1处有极值,
∴
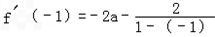 =0,
=0,解得a=﹣
 .
.(2)∵f(x)在[﹣3,﹣2)上是增函数,
∴
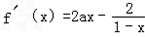 ≥0对一切x∈[﹣3,﹣2)恒成立,
≥0对一切x∈[﹣3,﹣2)恒成立,∴a≤
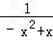 =
=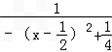 ,
,当x∈[﹣3,﹣2)时,﹣
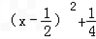 <﹣6,
<﹣6,∴
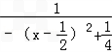 >﹣
>﹣ .
.故a≤﹣
 .
.(3)假设存在正数a,使得
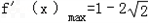 成立,
成立,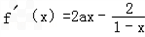 =2a﹣[2a(1﹣x)+
=2a﹣[2a(1﹣x)+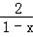 ]≤
]≤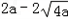 ,
,由2a(1﹣x)=
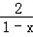 ,得(1﹣x)2=
,得(1﹣x)2= ,
,∴x=1±
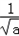 ,由于x=1+
,由于x=1+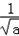 >1,故应舍去,
>1,故应舍去,当x=1﹣
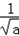 时,
时,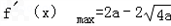 ,
,令2a﹣2
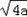 =1﹣2
=1﹣2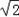 ,解得a=
,解得a= ,或a=
,或a=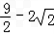 .
.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目