题目内容
已知函数
（其中x∈R，0＜φ＜π）的图象关于直线
对称．
（Ⅰ）求φ的值；
（Ⅱ）求函数f（x）的单调减区间．
解：（I）∵函数f（x）=sin（2x+
φ）
又y=sinx的图象的对称轴为x=
，k∈Z
令
，将x=
代入可得=
，k∈Z
∵0＜φ＜π
∴φ=
（II）由（I）知f（x）=sin（2x+
）
由
得
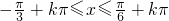，k∈Z
∴f（x）的单调递减区间为[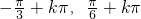
]（k∈Z）
分析：（I）利用两角和的正弦公式可得f（x）=sin（2x+φ），令，将x=结合0＜φ＜π可求
（II）由（I）知f（x）=sin（2x+），由可求
点评：本题主要考查了三角函数的两角和的正弦公式，三角函数的对称性及单调区间的求解，解题的关键是准确掌握正弦函数的性质并能灵活应用
φ）又y=sinx的图象的对称轴为x=
，k∈Z 令
，将x=代入可得=，k∈Z∵0＜φ＜π
∴φ=
（II）由（I）知f（x）=sin（2x+
）由
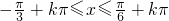得，k∈Z∴f（x）的单调递减区间为[
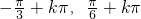]（k∈Z）分析：（I）利用两角和的正弦公式可得f（x）=sin（2x+
φ），令，将x=结合0＜φ＜π可求（II）由（I）知f（x）=sin（2x+
），由可求点评：本题主要考查了三角函数的两角和的正弦公式，三角函数的对称性及单调区间的求解，解题的关键是准确掌握正弦函数的性质并能灵活应用
练习册系列答案
口算能手系列答案
相关题目
（其中x∈R，A＞0，ω＞0）的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个点为
．
恒成立；q：函数y=（m2-1）x是增函数．若“p或q”为真，“p且q”为假，求实数m的取值范围．
（其中x∈R，A＞0，ω＞0）的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个点为
．
求函数f（x）的值域；
个单位，再将图象上各点的横坐标变为原来的2倍，纵坐标不变，求经以上变换后得到的函数解析式．
，其中x∈R，则下列结论中正确的是（ ）
的图象左移
得到函数f（x）的图象
，其中x∈R，则下列结论中正确的是（ ）
的图象左移
得到函数f（x）的图象
，其中x∈R，则下列结论中正确的是（ ）
的图象左移
得到函数f（x）的图象