题目内容
(本题满分14分)已知函数![]() .
.
(1)若![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且对于任意
,且对于任意![]() ,
,![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,求证:
,求证:![]() .
.
解:(1)由![]() 得
得![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ,故
,故![]() 的单调递增区间是
的单调递增区间是![]() ,
,
由![]() 得
得![]() ,故
,故![]() 的单调递减区间是
的单调递减区间是![]() .……………4分
.……………4分
(2)由![]() 可知
可知![]() 是偶函数.
是偶函数.
于是![]() 对任意
对任意![]() 成立等价于
成立等价于![]() 对任意
对任意![]() 成立.
成立.
由![]() 得
得![]() . ……………………………………6分
. ……………………………………6分
①当![]() 时,
时,![]() .
.
此时![]() 在
在![]() 上单调递增.
上单调递增.
故![]() ,符合题意. ……………………………………8分
,符合题意. ……………………………………8分
②当![]() 时,
时,![]() .
.
当![]() 变化时
变化时![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由此可得,在![]() 上,
上,![]() .
.
依题意,![]() ,又
,又![]() .
.
综合①,②得,实数![]() 的取值范围是
的取值范围是![]() .………………………10分
.………………………10分
【(方法二)由![]() 对任意
对任意![]() 成立等价于
成立等价于![]() 恒成立
恒成立
当![]() ,
,![]() 恒成立,则
恒成立,则![]() ,又
,又![]() ,所以此时
,所以此时![]() ………6分
………6分
当![]() ,
,![]() 恒成立,则
恒成立,则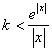 ,令
,令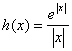 ,则
,则![]() ,……7分
,……7分
易知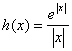 为
为![]() 上偶函数,考察
上偶函数,考察![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() ,所以
,所以![]() ……………………………9分
……………………………9分
综上![]() …………………………………………………………10分】
…………………………………………………………10分】
(3)![]() ,
,
![]()
![]() ,
,
…………………………………………………………11分
![]() ,
,
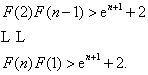 ……………………………………12分
……………………………………12分
由此得,![]() ………………………………………13分
………………………………………13分
故![]() . …………………………14分
. …………………………14分

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
