Question

（本小题满分12分）某公司对工厂A的一批产品进行了抽样检测。右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100),[100，102)，[102，104),[10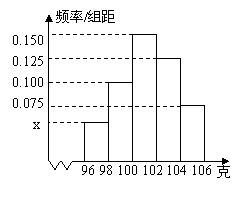4，106]。

（1）求图中x的值；

（2）若将频率视为概率，从这批产品中有放回地随机抽取3件，求至多有2件产品的净重在的概率；

（3）经过考察后，该公司决定在2011年年初投资到工厂A50万元，到年底可能获利，也可能亏损，且这两种情况发生的概率分别为合格产品和不合格产品的概率（若产品净重在为合格产品，其余为不合格产品）。设2011年底公司的投资总资产（本金+利润）为，求的分布列及数学期望。

Answer 1

（本小题满分12分）

解：（1）依题意及频率分布直方图知，，  2分

解得                                                 …………   3分

（2）法1：设所抽取到得产品的件数为X,由题意知，,因此

                        …………   5分

所以至多有2件产品的净重在的概率

。………   7分

法2：恰好抽取到3件产品的净重在的概率为

                                     …………   5分

所以至多有2件产品的净重在的概率

。                            …………   7分（3）法1：可能的值为：50×（1+32%）=66（万元）

                        50×（1－16%）=42（万元）                      …………   8分

                                    …………   10分

故的分布列为

                                                      …………   11分

（万元）.                         …………   12分

命题意图：本题主要考查频率分布直方图、二项分布、离散型随机变量的期望等知识，立足考查数据处理能力、计算能力和解决实际问题的能力．