题目内容
(2008•南京模拟)选修4-4:坐标系与参数方程
把参数方程
(t是参数)化为普通方程,并说明它表示什么曲线.
把参数方程
|
分析:将参数方程化为普通方程,其手段即为消参数,消参数要根据题设中条件选择方法
法一:对参数方程进行整理得
=x+1 ①,又
=y ②,两式相除得到t=
再代入
=x+1 即可消去参数得到普通方程;
法二:由题设,可令x=
,①,y=
②,观察其形式发现,由①2+(
)2即可消去参数,求得普通方程;
法一:对参数方程进行整理得
| 2 |
| t2+1 |
| 4t |
| t2+1 |
| y |
| 2(x+1) |
| 2 |
| t2+1 |
法二:由题设,可令x=
| 1-t2 |
| t2+1 |
| 4t |
| t2+1 |
| ② |
| 2 |
解答:解:法一:由x=
,得x=-1+
,即
=x+1 ①,又
=y ②,
②÷①得:t=
③,(3分)
将③代入①得 x+1=
,
整理得:x2+
=1. …(6分)
因为t2+1≥1,所以x=-1+
∈(-1,1],
所求普通方程为x2+
=1 (x≠-1).…(8分)
法二:由x=
,①,
y=
②,
①2+(
)2得x2+
=1. …(6分)
因为t2+1≥1,所以x=-1+
∈(-1,1],
所求普通方程为x2+
=1 (x≠-1).…(8分)
| 1-t2 |
| t2+1 |
| 2 |
| t2+1 |
| 2 |
| t2+1 |
| 4t |
| t2+1 |
②÷①得:t=
| y |
| 2(x+1) |
将③代入①得 x+1=
| 2 | ||
(
|
整理得:x2+
| y2 |
| 4 |
因为t2+1≥1,所以x=-1+
| 2 |
| t2+1 |
所求普通方程为x2+
| y2 |
| 4 |
法二:由x=
| 1-t2 |
| t2+1 |
y=
| 4t |
| t2+1 |
①2+(
| ② |
| 2 |
| y2 |
| 4 |
因为t2+1≥1,所以x=-1+
| 2 |
| t2+1 |
所求普通方程为x2+
| y2 |
| 4 |
点评:本题考查将参数方程化为普通方程,考查了代入法消去参数与组合法消去参数,解题的关键是掌握住消去参数的方法原理,方法一代入法法消去参数是常规方法,具有一般性,方法二通过对形式组合整体消去参数,技巧性较高,需要答题者有较强的观察能力及对条件进行变形整理的能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
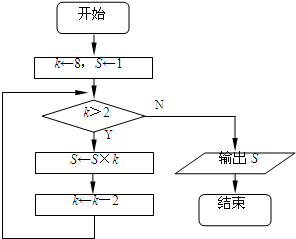 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是