题目内容
已知函数 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)在区间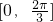 上的取值范围.
上的取值范围.
(Ⅲ)函数f(x)的图象可由y=sinx的图象经过怎样的变化得到?
解:(Ⅰ)由题意知,
= =
=
∵f(x)的最小正周期为π,且ω>0
∴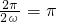 ,∴ω=1
,∴ω=1
(Ⅱ)解:
∵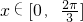 ,∴
,∴ ,
,
∴ ,∴
,∴
∴
即f(x)在区间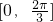 上的取值范围是
上的取值范围是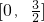 .
.
(Ⅲ)解:把y=sinx的图象上所有点的横坐标缩短为原来的 倍(纵坐标不变),
倍(纵坐标不变),
再把所得函数的图象向右平移 个单位,
个单位,
再把所得函数的图象向上平移 个单位,可得到f(x)的图象.
个单位,可得到f(x)的图象.
分析:(Ⅰ)根据解析式需要利用倍角公式和两角和的正弦公式对解析式进行化简,再由周期公式
 求出ω的值;
求出ω的值;(Ⅱ)根据(Ⅰ)求出的解析式,由x的范围求出2x-
 的范围,根据正弦函数的性质求出函数的值域;
的范围,根据正弦函数的性质求出函数的值域;(Ⅲ)根据图象的变换过程,先周期变换再相位变换,最后上下平移,注意左右平移的单位长度.
点评:本题的考点是图象的变换和解析式的求法,应先对解析式化简再把条件代入,利用知识点有倍角公式和两角和的正弦公式,图象变换法则和正弦函数的性质,考查了整体思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (-1≤x≤0)的反函数是( )
(-1≤x≤0)的反函数是( )




 的定义域是 ;
的定义域是 ; 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 .  终边经过点P(-4,3),求
终边经过点P(-4,3),求 的值?
的值? ,(b>0)在
,(b>0)在 的最大值为
的最大值为 ,最小值为-
,最小值为- ,求2a+b的值?
,求2a+b的值? ,(ω>0)的最小正周期为4π.
,(ω>0)的最小正周期为4π. (w>0)的图象的两相邻对称轴间的距离为
(w>0)的图象的两相邻对称轴间的距离为 .
. ,且f(x)=m有且仅有一个实根,求实数m的值.
,且f(x)=m有且仅有一个实根,求实数m的值.