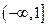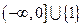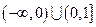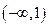题目内容
(本小题满分15分)已知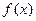 是定义在
是定义在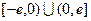 上的奇函数,当
上的奇函数,当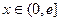 时,
时,
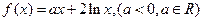
(1)求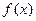 的解析式;
的解析式;
(2)是否存在实数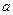 ,使得当
,使得当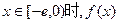 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出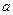 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
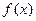 是定义在
是定义在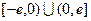 上的奇函数,当
上的奇函数,当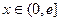 时,
时,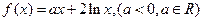
(1)求
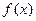 的解析式;
的解析式;(2)是否存在实数
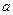 ,使得当
,使得当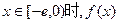 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出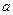 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。(1)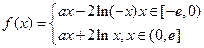
(2)存在实数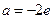 ,使得当
,使得当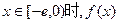 最小值4。
最小值4。
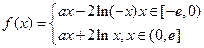
(2)存在实数
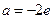 ,使得当
,使得当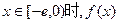 最小值4。
最小值4。(1)设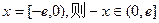
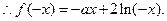
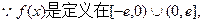 上的奇函数,
上的奇函数,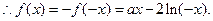
故函数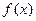 的解析式为:
的解析式为: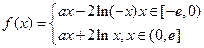
(2)假设存在实数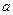 ,使得当
,使得当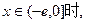
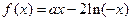 有最小值是3。
有最小值是3。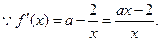
①当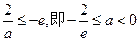 时,
时,
由于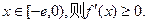 故函数
故函数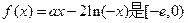 上的增函数。
上的增函数。
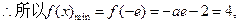 解得
解得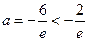 (舍去)
(舍去)
②当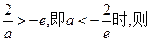
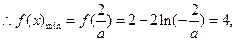 解得
解得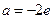
综上所知,存在实数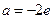 ,使得当
,使得当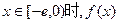 最小值4。
最小值4。
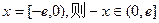
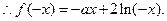
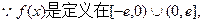 上的奇函数,
上的奇函数,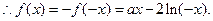
故函数
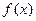 的解析式为:
的解析式为: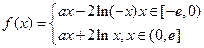
(2)假设存在实数
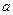 ,使得当
,使得当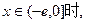
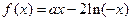 有最小值是3。
有最小值是3。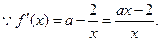
①当
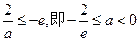 时,
时,由于
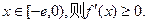 故函数
故函数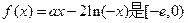 上的增函数。
上的增函数。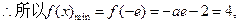 解得
解得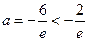 (舍去)
(舍去)②当
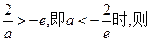
| x | 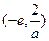 | 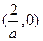 |
 | — | + |
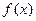 | ↘ | ↗ |
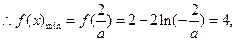 解得
解得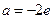
综上所知,存在实数
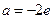 ,使得当
,使得当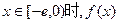 最小值4。
最小值4。
练习册系列答案
相关题目
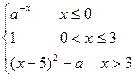 ( a > 0且a ≠1)图象经过点Q(8, 6).
( a > 0且a ≠1)图象经过点Q(8, 6). )试将利润y表示为x的函数,并求出上涨几元,可获最大利润.
)试将利润y表示为x的函数,并求出上涨几元,可获最大利润. 方程
方程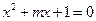 有两
有两 个不等的正实数根,命题
个不等的正实数根,命题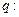 函数
函数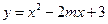 在区间
在区间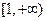 上单调递增. 若命题“
上单调递增. 若命题“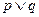 ”是真命题,命题“
”是真命题,命题“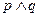 ”是假命题,求实数
”是假命题,求实数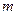 的取值范围.
的取值范围.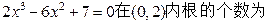 ( )
( )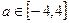 ,
,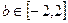 ,并且二次方程
,并且二次方程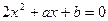 有实根,则方程的根均在区间
有实根,则方程的根均在区间 内的概率为( )
内的概率为( )
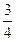

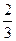
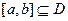 ,使得f(x)在[a,b]上的值域为[a,b],则y=f(x)叫做闭函数。现在
,使得f(x)在[a,b]上的值域为[a,b],则y=f(x)叫做闭函数。现在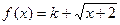 是闭函数,则k的取值范围是( )
是闭函数,则k的取值范围是( )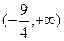
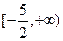
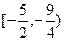
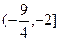
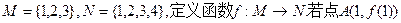 、
、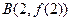 、
、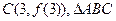 的外接圆圆心为D,且
的外接圆圆心为D,且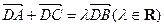 ,则满足条件的函数
,则满足条件的函数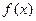 有 ( )
有 ( )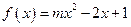 有且仅有一个正实数的零点,则实数
有且仅有一个正实数的零点,则实数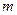 的取值范围是( )
的取值范围是( )