题目内容
在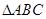 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为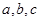 ,已知向量
,已知向量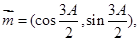
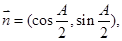 且满足
且满足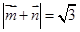 .
.
(1)求角A的大小;
(2)若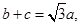 试判断
试判断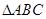 的形状.
的形状.
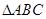 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为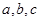 ,已知向量
,已知向量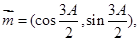
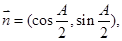 且满足
且满足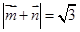 .
.(1)求角A的大小;
(2)若
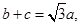 试判断
试判断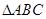 的形状.
的形状.(1) ; (2)
; (2) 为直角三角形.
为直角三角形.
 ; (2)
; (2) 为直角三角形.
为直角三角形.试题分析:(1)通过向量的坐标运算,易得
 的长度为1,由
的长度为1,由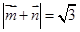 ,可得
,可得 ,再利用数量积的坐标运算可得
,再利用数量积的坐标运算可得 ,可得A;(2)由正弦定理将
,可得A;(2)由正弦定理将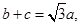 转化成角的正弦的关系,结合A的度数可求得B,C的度数,进而判断出三角形的形状.
转化成角的正弦的关系,结合A的度数可求得B,C的度数,进而判断出三角形的形状.试题解析:
解


 6分
6分



所以:
 为直角三角形. 13分
为直角三角形. 13分
练习册系列答案
相关题目
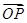 =
=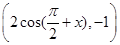 ,
,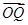 =
=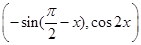 ,定义函数f(x)=
,定义函数f(x)=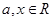 ,函数
,函数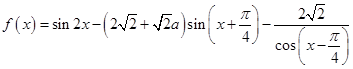 .
.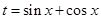 ,将函数
,将函数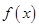 表示为关于
表示为关于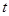 的函数
的函数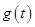 ,求
,求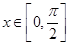 ,不等式
,不等式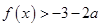 都成立,求实数
都成立,求实数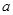 的取值范围.
的取值范围.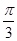 ”是“cos θ≠
”是“cos θ≠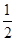 ”的( )
”的( )
 .
.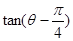 的值;
的值;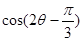 的值.
的值.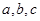 ,若
,若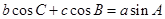 ,则△ABC的形状为( )
,则△ABC的形状为( )
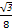
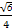
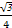
 ,
, ,且
,且 ,则向量a,b的夹角是( )
,则向量a,b的夹角是( )


