题目内容

设f（x）=3-x-ln

2x+1

，实数a，b，c满足f（a）f（b）f（c）＜0，且0＜a＜b＜c，若x₀是函数的一个零点，下列不等式中不可能成立的为（　　）

A．x₀＜a

B．x₀＞b

C．x₀＞c

D．x₀＜c

∵f（x）=3-x-ln

2x+1

=

1

3x

-ln

2x+1

（x＞-

1

2

）
∵0＜a＜b＜c，且 f（a）f（b）f（c）＜0，
∴f（a）、f（b）、f（c）中一项为负的、两项为正的；或者三项都是负的．
即f（c）＜0，0＜f（b）＜f（a）；或f（a）＜f（b）＜f（c）＜0．
由于实数x₀是函数y=f（x）的一个零点，
当f（c）＜0，0＜f（b）＜f（a）时，b＜x₀＜c，此时B，D成立．
当f（a）＜f（b）＜f（c）＜0时，x₀＜a，此时A成立．
综上可得，C不可能成立，
故选C；

练习册系列答案

英语指导系列答案

龙江中考系列答案

状元陪练系列答案

2016中考168系列答案

创新设计导学课堂系列答案

创新设计学业水平考试系列答案

金状元直击期末系列答案

小学生智能优化卷系列答案

师大测评卷提炼知识点系列答案

挑战100分期末天天练系列答案

相关题目

设定义在R上的函数f（x）对于任意x，y都有f（x+y）=f（x）+f（y）成立，且f（1）=-2，当x＞0时，f（x）＜0
（1）判断f（x）的奇偶性，并加以证明；
（2）试问：当-3≤x=0≤3时，x=1是否有最值？如果有，求出最值；如果没有，说明理由．

设f（x）=3-x-ln

，实数a，b，c满足f（a）f（b）f（c）＜0，且0＜a＜b＜c，若x₀是函数的一个零点，下列不等式中不可能成立的为（　　）

已知f 1(x)=|3x-1|，f2(x)=|a•3x-9|(a＞0)，x∈R，且f（x）=

f1(x)，f1(x)≤f2(x)

f2(x)，f1(x)＞f2(x)

（1）当a=1时，求f（x）的解析式；
（2）在（1）的条件下，若方程f（x）-m=0有4个不等的实根，求实数m的范围；
（3）当2≤a＜9时，设f（x）=f₂（x）所对应的自变量取值区间的长度为l（闭区间[m，n]的长度定义为n-m），试求l的最大值．

设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x³-4x+3．有下列命题：
①f(-

)；
②当x∈[-1，0]时f（x）=x³+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）

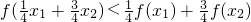设f（x）是定义在集合D上的函数，若对集合D中的任意两数x₁，x₂恒有 $数学公式$ 成立，则f（x）是定义在D上的β函数．
（1）试判断f（x）=x²是否是其定义域上的β函数？
（2）设f（x）是定义在R上的奇函数，求证：f（x）不是定义在R上的β函数．
（3）设f（x）是定义在集合D上的函数，若对任意实数α∈[0，1]以及集合D中的任意两数x₁，x₂恒有f（αx₁+（1-α）x₂）≤αf（x₁）+（1-α）f（x₂），则称f（x）是定义在D上的α-β函数．已知f（x）是定义在R上的α-β函数，m是给定的正整数，设a_n=f（n），n=1，2，3…m且a₀=0，a_m=2m，记∫=a₁+a₂+a₃+…+a_m，对任意满足条件的函数f（x），求∫的最大值．