题目内容
有三位学生等可能地选择A、B、C、D四种不同的数学参考资料中的一种，则三位学生选择的数学参考资料互不相同的概率为
．
| 3 |
| 8 |
| 3 |
| 8 |
分析：三位学生等可能地选择A、B、C、D四种不同的数学参考资料中的一种，每一人都有4种选择，总共有43，互不相同的则有A43，代入概率公式可得答案．
解答：解：三位学生等可能地选择A、B、C、D四种不同的数学参考资料中的一种，
每一人都有4种选择，
总共有43种不同的方法
若三位学生选择的数学参考资料互不相同
共有A43种不同的选择方法
故三位学生选择的数学参考资料互不相同的概率P=
=
故答案
．
每一人都有4种选择，
总共有43种不同的方法
若三位学生选择的数学参考资料互不相同
共有A43种不同的选择方法
故三位学生选择的数学参考资料互不相同的概率P=
| ||
| 43 |
| 3 |
| 8 |
故答案
| 3 |
| 8 |
点评：本题考查的知识点是古典概型及其概率计算公式，其中根据分步原理和排列公式求出事件总数及满足条件的基本事件个数是解答的关键．
练习册系列答案
相关题目
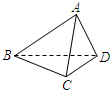如图，已知正四面体ABCD的棱长为3cm．
