题目内容
已知函数f(x)=log3(ax+b)的图象经过点A(2,1)和B(5,2),记an=3f(n),n∈N*.
(1)求数列{an}的通项公式;
(2)设 ,,求Tn.
,,求Tn.
解:(1)由题意得 ,解得
,解得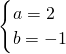 ,∴f(x)=log3(2x-1)
,∴f(x)=log3(2x-1)
(2)由(1)得 ,∴
,∴ ①
① ②;
②;
①-②得 =
= ,
,
∴
分析:(1)由题意得 ,解得
,解得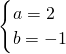 ,所以f(x)=log3(2x-1),由此能求出数列{an}的通项公式.
,所以f(x)=log3(2x-1),由此能求出数列{an}的通项公式.
(2)由 ,得
,得 ,再由错位相减法能够得到Tn.
,再由错位相减法能够得到Tn.
点评:本题考查数列的递推公式和前n项和的求解,解题时要认真审题,注意函数思想和错位相减求和法的合理运用.
 ,解得
,解得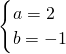 ,∴f(x)=log3(2x-1)
,∴f(x)=log3(2x-1)
(2)由(1)得
 ,∴
,∴ ①
① ②;
②;①-②得
 =
= ,
,∴

分析:(1)由题意得
 ,解得
,解得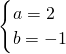 ,所以f(x)=log3(2x-1),由此能求出数列{an}的通项公式.
,所以f(x)=log3(2x-1),由此能求出数列{an}的通项公式.(2)由
 ,得
,得 ,再由错位相减法能够得到Tn.
,再由错位相减法能够得到Tn.点评:本题考查数列的递推公式和前n项和的求解,解题时要认真审题,注意函数思想和错位相减求和法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目