题目内容
以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是
- A.x2-y2=2
- B.y2-x2=2
- C.x2-y2=4或y2-x2=4
- D.x2-y2=2或y2-x2=2
D
分析:首先根据焦点在不同的坐标轴上分别设出双曲线的方程,然后由焦点在x轴上的双曲线的渐近线方程为y=± x,准线方程为x=
x,准线方程为x= ,焦点在y轴上的双曲线的方程为y=
,焦点在y轴上的双曲线的方程为y=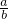 x,准线方程为y=
x,准线方程为y= ,且均有性质c2=a2+b2,则列出方程组分别解之即可.
,且均有性质c2=a2+b2,则列出方程组分别解之即可.
解答:若双曲线的焦点在x轴上,设其方程为 ,
,
因为它的渐近线方程为y=± x,准线方程为x=
x,准线方程为x= ,
,
所以 ,解得a2=b2=2,
,解得a2=b2=2,
所以焦点在x轴上的双曲线的方程为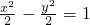 ;
;
同理设焦点在y轴上的双曲线的方程为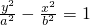 ,
,
则 ,解得a2=b2=2,
,解得a2=b2=2,
所以焦点在y轴上的双曲线的方程为 .
.
因此满足要求的双曲线的方程为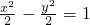 或
或  .
.
故选D.
点评:本题主要考查焦点在不同坐标轴上的双曲线的标准方程及性质,同时考查解方程组的能力,此题要注意分别设在x轴和y轴上的双曲线方程进行解答.属于基础题.
分析:首先根据焦点在不同的坐标轴上分别设出双曲线的方程,然后由焦点在x轴上的双曲线的渐近线方程为y=±
 x,准线方程为x=
x,准线方程为x= ,焦点在y轴上的双曲线的方程为y=
,焦点在y轴上的双曲线的方程为y=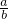 x,准线方程为y=
x,准线方程为y= ,且均有性质c2=a2+b2,则列出方程组分别解之即可.
,且均有性质c2=a2+b2,则列出方程组分别解之即可.解答:若双曲线的焦点在x轴上,设其方程为
 ,
,因为它的渐近线方程为y=±
 x,准线方程为x=
x,准线方程为x= ,
,所以
 ,解得a2=b2=2,
,解得a2=b2=2,所以焦点在x轴上的双曲线的方程为
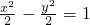 ;
;同理设焦点在y轴上的双曲线的方程为
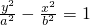 ,
,则
 ,解得a2=b2=2,
,解得a2=b2=2,所以焦点在y轴上的双曲线的方程为
 .
.因此满足要求的双曲线的方程为
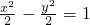 或
或  .
.故选D.
点评:本题主要考查焦点在不同坐标轴上的双曲线的标准方程及性质,同时考查解方程组的能力,此题要注意分别设在x轴和y轴上的双曲线方程进行解答.属于基础题.

练习册系列答案
相关题目
以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是( )
| A、x2-y2=2 | B、y2-x2=2 | C、x2-y2=4或y2-x2=4 | D、x2-y2=2或y2-x2=2 |