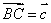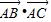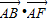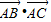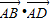题目内容
 如图,在边长为1的正方形OABC内取一点P(x,y),求:
如图,在边长为1的正方形OABC内取一点P(x,y),求:(1)点P到原点距离小于1的概率;
(2)以x,y,1为边长能构成三角形的概率;
(3)以x,y,1为边长能构成锐角三角形的概率.
分析:(1)点P到原点距离小于1,则P位于以O为圆心、半径为1的圆内部,因此所求概率等于如图的扇形面积与正方形ABCO的面积之比,由此即可算出P到原点距离小于1的概率;
(2)以x、y、1为边长能构成三角形,则P位于的区域为如图的△ABC及其内部,因此用△ABC面积除以正方形ABCO的面积,即可得到以x、y、1为边长能构成三角形的概率;
(3)以x、y、1为边长能构成锐角三角形,则P位于的区域为正方形ABCO内部且位于以O为圆心、半径为1的圆外部,即如图的阴影部分,由此即可算出以x、y、1为边长能构成锐角三角形的概率.
(2)以x、y、1为边长能构成三角形,则P位于的区域为如图的△ABC及其内部,因此用△ABC面积除以正方形ABCO的面积,即可得到以x、y、1为边长能构成三角形的概率;
(3)以x、y、1为边长能构成锐角三角形,则P位于的区域为正方形ABCO内部且位于以O为圆心、半径为1的圆外部,即如图的阴影部分,由此即可算出以x、y、1为边长能构成锐角三角形的概率.
解答: 解:(1)若点P到原点距离小于1,则P位于以O为圆心、半径为1的圆内部
解:(1)若点P到原点距离小于1,则P位于以O为圆心、半径为1的圆内部
因此,点P到原点距离小于1的概率为P1=
=
(3分)
(2)若以x,y,1为边长能构成三角形,
则有
,
对应区域为正方形ABCO内部且位于直线AC上方,即△ABC及其内部,
因此以x、y、1为边长能构成三角形的概率为P2=
=
(6分)
(3)以x,y,1为边长能构成锐角三角形,注意到最长的边等于1
可得
,
对应区域为正方形ABCO内部且位于以O为圆心、半径为1的圆外部,即如图的阴影部分
因此以x,y,1为边长能构成锐角三角形的概率为
P3=
=1-
(10分)
答:(1)点P到原点距离小于1的概率为
;
(2)以x,y,1为边长能构成三角形的概率为
;
(3)以x,y,1为边长能构成锐角三角形的概率为1-
.(12分)
 解:(1)若点P到原点距离小于1,则P位于以O为圆心、半径为1的圆内部
解:(1)若点P到原点距离小于1,则P位于以O为圆心、半径为1的圆内部因此,点P到原点距离小于1的概率为P1=
| ||
| 1×1 |
| π |
| 4 |
(2)若以x,y,1为边长能构成三角形,
则有
|

对应区域为正方形ABCO内部且位于直线AC上方,即△ABC及其内部,
因此以x、y、1为边长能构成三角形的概率为P2=
| S△ABC |
| SABCO |
| 1 |
| 2 |
(3)以x,y,1为边长能构成锐角三角形,注意到最长的边等于1
可得
|

对应区域为正方形ABCO内部且位于以O为圆心、半径为1的圆外部,即如图的阴影部分
因此以x,y,1为边长能构成锐角三角形的概率为
P3=
1×1-
| ||
| 1×1 |
| π |
| 4 |
答:(1)点P到原点距离小于1的概率为
| π |
| 4 |
(2)以x,y,1为边长能构成三角形的概率为
| 1 |
| 2 |
(3)以x,y,1为边长能构成锐角三角形的概率为1-
| π |
| 4 |
点评:本题给出点P在以O(0,0)、A(1,0)、B(1,1)、C(0,1)为顶点的正方形内部运动,求以P的坐标x、y为两边,1为第三边能构成三角形的概率.着重考查了扇形面积公式、正方形面积公式和几何概型计算公式等知识,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
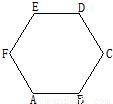
如图,在边长为1的正六边形ABCDEF中,下列向量的数量积中最大的是( )
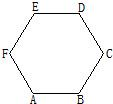

A、
| ||||
B、
| ||||
C、
| ||||
D、
|