题目内容
已知 ,g(x)=x+a (a>0)
,g(x)=x+a (a>0)
(1)当a=4时,求 的最小值
的最小值
(2)当1≤x≤4时,不等式 >1恒成立,求a的取值范围.
>1恒成立,求a的取值范围.
解:(1)当a=4时,
∵ ,∴
,∴ ,
, ,取“=”号
,取“=”号
故 的最小值为15;
的最小值为15;
(2) (1≤x≤4)
(1≤x≤4)
设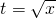 ,则问题等价于
,则问题等价于 ,t∈[1,2]时恒成立,
,t∈[1,2]时恒成立,
即 或
或 ,t∈[1,2]时恒成立,
,t∈[1,2]时恒成立,
令 ,则只需h(t)在[1,2]上的最小值大于2或最大值小于0即可,
,则只需h(t)在[1,2]上的最小值大于2或最大值小于0即可,
由函数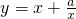 的单调性知
的单调性知  ,
,
 或a<0
或a<0
解得a>1或a<0
分析:(1)当a=4时,先研究函数 的值域,再求
的值域,再求 的最小值;
的最小值;
(2)首先可化简为 (1≤x≤4),设
(1≤x≤4),设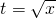 ,则问题等价于
,则问题等价于 ,t∈[1,2]时恒成立,即
,t∈[1,2]时恒成立,即 或
或 ,t∈[1,2]时恒成立,再考查对勾函数的单调性,从而建立不等式,求解即可.
,t∈[1,2]时恒成立,再考查对勾函数的单调性,从而建立不等式,求解即可.
点评:本题的考点是函数恒成立问题,考查学生基本不等式在最值问题中的应用、利用整体代换的数学思想解决数学问题的能力,以及不等式恒成立的证明方法.

∵
 ,∴
,∴ ,
, ,取“=”号
,取“=”号故
 的最小值为15;
的最小值为15;(2)
 (1≤x≤4)
(1≤x≤4)设
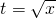 ,则问题等价于
,则问题等价于 ,t∈[1,2]时恒成立,
,t∈[1,2]时恒成立,即
 或
或 ,t∈[1,2]时恒成立,
,t∈[1,2]时恒成立,令
 ,则只需h(t)在[1,2]上的最小值大于2或最大值小于0即可,
,则只需h(t)在[1,2]上的最小值大于2或最大值小于0即可,由函数
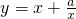 的单调性知
的单调性知  ,
, 或a<0
或a<0解得a>1或a<0
分析:(1)当a=4时,先研究函数
 的值域,再求
的值域,再求 的最小值;
的最小值;(2)首先可化简为
 (1≤x≤4),设
(1≤x≤4),设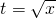 ,则问题等价于
,则问题等价于 ,t∈[1,2]时恒成立,即
,t∈[1,2]时恒成立,即 或
或 ,t∈[1,2]时恒成立,再考查对勾函数的单调性,从而建立不等式,求解即可.
,t∈[1,2]时恒成立,再考查对勾函数的单调性,从而建立不等式,求解即可.点评:本题的考点是函数恒成立问题,考查学生基本不等式在最值问题中的应用、利用整体代换的数学思想解决数学问题的能力,以及不等式恒成立的证明方法.

练习册系列答案
相关题目
已知函数f(x)、g(x),下列说法正确的是( )
| A、f(x)是奇函数,g(x)是奇函数,则f(x)+g(x)是奇函数 | B、f(x)是偶函数,g(x)是偶函数,则f(x)+g(x)是偶函数 | C、f(x)是奇函数,g(x)是偶函数,则f(x)+g(x)一定是奇函数或偶函数 | D、f(x)是奇函数,g(x)是偶函数,则f(x)+g(x)可以是奇函数或偶函数 |