题目内容
(14分) 某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:方案一:年平均获利最大时,以26万元出售该渔船;方案二:总纯收入获利最大时,以8万元出售该渔船.问哪种方案合算?
(14分) 某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年都增加4万元,每年捕鱼收益50万元.(1)问第几年开始获利?(2)若干年后,有两种处理方案:方案一:年平均获利最大时,以26万元出售该渔船;方案二:总纯收入获利最大时,以8万元出售该渔船.问哪种方案合算?
解:(1)由题意知,每年的费用是以12为首项,4为公差的等差数列.
设纯收入与年数n的关系为f(n),则![]() …
…![]() .
.
由题知获利即为f(n)>0,由![]() ,得
,得![]()
![]() .
.
∵n![]() N,∴n=3,4,5,…,17.即第3年开始获利.
N,∴n=3,4,5,…,17.即第3年开始获利.
(2)方案一:年平均收入![]() .
.
由于![]() ,当且仅当n=7时取“=”号.∴
,当且仅当n=7时取“=”号.∴ ![]() (万元).
(万元).
即前7年年平均收益最大,此时总收益为12×7+26=110(万元).
方案二:f(n)=![]() +40n-98=-2
+40n-98=-2![]() +102.
+102.
当n=10时,f(n)取最大值102,此时总收益为102+8=110(万元).
比较如上两种方案,总收益均为110万元,而方案一中n=7,故选方案一.

| |||||||||||
(09年大丰调研)(14分) 某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价![]() (元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
时间(将第x天记为x)x | 1 | 10 | 11 | 18 |
单价(元/件)P | 9 | 0 | 1 | 8 |
而这20天相应的销售量![]() (百件/天)与
(百件/天)与![]() 对应的点
对应的点![]() 在如图所示的半圆上.
在如图所示的半圆上.
![]() (Ⅰ)写出每天销售收入
(Ⅰ)写出每天销售收入![]() (元)与时间
(元)与时间![]() (天)的函数关系式
(天)的函数关系式![]() ;
;
![]() (Ⅱ)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价
(Ⅱ)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价![]() 定为多少元为好?(结果精确到1元)
定为多少元为好?(结果精确到1元)
![]()

![]()
![]()
![]()
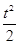 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).