题目内容
已知函数f(x)=lg(x2-x-2),若?a、b∈(m,+∞),都有[f(a)-f(b)](a-b)>0,则实数m最小值是________.
2
分析:由?a、b∈(m,+∞),都有[f(a)-f(b)](a-b)>0,知f(x)在(m,+∞)上单调递增,则(m,+∞)为函数f(x)增区间的子集,根据复合函数单调性的判断方法求出f(x)的增区间,由集合包含关系可得m的范围,注意函数定义域;
解答:由x2-x-2>0解得x<-1或x>2,
所以函数f(x)的定义域为(-∞,-1)∪(2,+∞),
y=x2-x-2=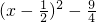 在(-∞,
在(-∞, )上递减,在(
)上递减,在( ,+∞)上递增,
,+∞)上递增,
又x<-1或x>2,
所以y=x2-x-2的减区间为(-∞,-1),增区间为(2,+∞),
而y=lgu递增,
所以f(x)的减区间为(-∞,-1),增区间为(2,+∞),
由?a、b∈(m,+∞),都有[f(a)-f(b)](a-b)>0,知f(x)在(m,+∞)上单调递增,
所以(m,+∞)⊆(2,+∞),故m≥2,
所以实数m的最小值为2,
故答案为:2.
点评:本题考查函数单调性定义及复合函数单调性的判断,复合函数单调性的判断方法为“同增异减”.
分析:由?a、b∈(m,+∞),都有[f(a)-f(b)](a-b)>0,知f(x)在(m,+∞)上单调递增,则(m,+∞)为函数f(x)增区间的子集,根据复合函数单调性的判断方法求出f(x)的增区间,由集合包含关系可得m的范围,注意函数定义域;
解答:由x2-x-2>0解得x<-1或x>2,
所以函数f(x)的定义域为(-∞,-1)∪(2,+∞),
y=x2-x-2=
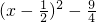 在(-∞,
在(-∞, )上递减,在(
)上递减,在( ,+∞)上递增,
,+∞)上递增,又x<-1或x>2,
所以y=x2-x-2的减区间为(-∞,-1),增区间为(2,+∞),
而y=lgu递增,
所以f(x)的减区间为(-∞,-1),增区间为(2,+∞),
由?a、b∈(m,+∞),都有[f(a)-f(b)](a-b)>0,知f(x)在(m,+∞)上单调递增,
所以(m,+∞)⊆(2,+∞),故m≥2,
所以实数m的最小值为2,
故答案为:2.
点评:本题考查函数单调性定义及复合函数单调性的判断,复合函数单调性的判断方法为“同增异减”.

练习册系列答案
相关题目