Question

已知点,的坐标分别是，.直线,相交于点，且它们的斜率之积为.

（1）求点的轨迹的方程；

（2）若过点的两直线和与轨迹都只有一个交点，且,求的值;

(3)在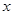轴上是否存在两个定点,,使得点到点的距离与到点的距离的比恒为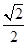,若存在，求出定点,；若不存在，请说明理由.

 

Answer 1

【答案】

（1）轨迹的方程为 

（2）

（3）存在定点，或，

【解析】

试题分析：解： （1）设点的坐标为

由题可知,即，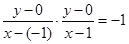

化简得 ，

所以点的轨迹的方程为                                 4分

（2）分四种情况讨论

情况一：当直线和都与相切时，直线和与轨迹都只有一个交点。

设直线的方程为，即

由可知直线的方程为，即

因为直线和都与相切，所以 解得。             6分

情况二：当直线过点,直线过点时，直线和与轨迹都只有一个交点。

此时直线的斜率，直线的斜率

由知，解得。                                       7分

情况三：当直线过点,直线与相切时，直线和与轨迹都只有一个交点。

直线的斜率，由知直线的斜率

故直线的方程为，即

因为直线与相切，所以 解得。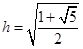

情况四：当直线过点,直线与相切时，直线和与轨迹都只有一个交点。

直线的斜率，由知直线的斜率

故直线的方程为，即

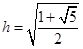因为直线与相切，所以 解得。               10分

综上所述：的值为，1，。

（3）假设存在定点,,设，，

则化简整理得（*）         11分

由于满足，故（*）式可化为        12分

故解得或                                

故存在定点，或，，使得点到点的距离与到点的距离的比为。                                                              14分

考点：轨迹方程，直线与圆的位置关系

点评：主要是考查了直线与原点位置关系的运用，以及轨迹方程的求解，属于中档题。