题目内容
已知a>0,且a≠1,函数f(x)=loga(1-ax),
(Ⅰ)求函数f(x)的定义域,并判断f(x)的单调性;
(Ⅱ)若n∈N*,求 ;
;
(Ⅲ)当a=e(e为自然对数的底数)时,设h(x)=(1-ef(x))(x2-m+1),若函数h(x)的极值存在,求实数m的取值范围以及函数h(x)的极值。
(Ⅰ)求函数f(x)的定义域,并判断f(x)的单调性;
(Ⅱ)若n∈N*,求
 ;
;(Ⅲ)当a=e(e为自然对数的底数)时,设h(x)=(1-ef(x))(x2-m+1),若函数h(x)的极值存在,求实数m的取值范围以及函数h(x)的极值。
解:(Ⅰ)由题意知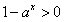 ,
,
当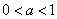 时,f(x)的定义域为
时,f(x)的定义域为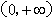 ;当a>1时,f(x)的定义域为
;当a>1时,f(x)的定义域为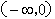 ,
,
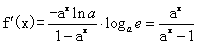 ,
,
当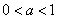 时,x∈
时,x∈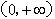 ,
,
因为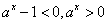 ,故f′(x)<0,所以f(x)是减函数;
,故f′(x)<0,所以f(x)是减函数;
当a>1时,x∈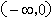 ,
,
因为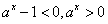 ,故f′(x)<0,所以f(x)是减函数;
,故f′(x)<0,所以f(x)是减函数;
(Ⅱ)因为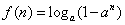 ,所以
,所以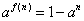 ,
,
由函数定义域知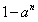 >0,
>0,
因为n是正整数,故0<a<1,
所以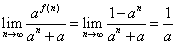 ;
;
(Ⅲ)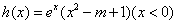 ,
,
所以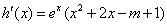 ,
,
令h′(x)=0,即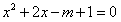 ,由题意应有△≥0,即m≥0,
,由题意应有△≥0,即m≥0,
①当m=0时,h′(x)=0有实根x=-1,在x=-1点左右两侧均有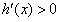 ,故无极值;
,故无极值;
②当0<m<1时,h′(x)=0有两个实根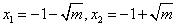 ,
,
当x变化时,h′(x)、h(x)的变化情况如下表所示:

∴h(x)的极大值为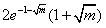 ,h(x)的极小值为
,h(x)的极小值为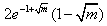 ;
;
③当m≥1时,h′(x)=0在定义域内有一个实根,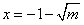 ,
,
同上可得h(x)的极大值为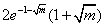 ;
;
综上所述,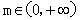 时,函数h(x)有极值,
时,函数h(x)有极值,
当0<m<1时h(x)的极大值为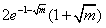 ,h(x)的极小值为
,h(x)的极小值为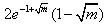 ;当m≥1时,h(x)的极大值为
;当m≥1时,h(x)的极大值为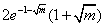 。
。
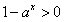 ,
,当
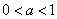 时,f(x)的定义域为
时,f(x)的定义域为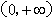 ;当a>1时,f(x)的定义域为
;当a>1时,f(x)的定义域为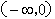 ,
,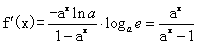 ,
,当
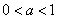 时,x∈
时,x∈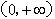 ,
,因为
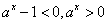 ,故f′(x)<0,所以f(x)是减函数;
,故f′(x)<0,所以f(x)是减函数;当a>1时,x∈
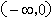 ,
,因为
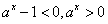 ,故f′(x)<0,所以f(x)是减函数;
,故f′(x)<0,所以f(x)是减函数;(Ⅱ)因为
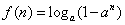 ,所以
,所以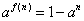 ,
,由函数定义域知
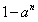 >0,
>0,因为n是正整数,故0<a<1,
所以
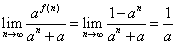 ;
;(Ⅲ)
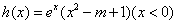 ,
,所以
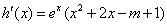 ,
,令h′(x)=0,即
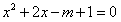 ,由题意应有△≥0,即m≥0,
,由题意应有△≥0,即m≥0,①当m=0时,h′(x)=0有实根x=-1,在x=-1点左右两侧均有
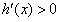 ,故无极值;
,故无极值;②当0<m<1时,h′(x)=0有两个实根
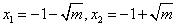 ,
,当x变化时,h′(x)、h(x)的变化情况如下表所示:

∴h(x)的极大值为
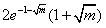 ,h(x)的极小值为
,h(x)的极小值为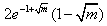 ;
;③当m≥1时,h′(x)=0在定义域内有一个实根,
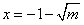 ,
,同上可得h(x)的极大值为
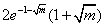 ;
;综上所述,
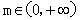 时,函数h(x)有极值,
时,函数h(x)有极值,当0<m<1时h(x)的极大值为
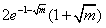 ,h(x)的极小值为
,h(x)的极小值为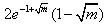 ;当m≥1时,h(x)的极大值为
;当m≥1时,h(x)的极大值为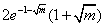 。
。
练习册系列答案
相关题目
 .
. .
.